一、模拟信号转化为数字信号
在数字信号的文章中我们说到，只有经过人为加工，才能使信号离散化。但对这个加工过程，却没有进一步解释。那么，本期文章我们就来看看，模拟信号是如何转化为数字信号的。
1、采样
首先要对模拟信号进行采样，一般以固定周期的采样脉冲采集模拟信号，这样就可以得到一个在时间上离散的信号。
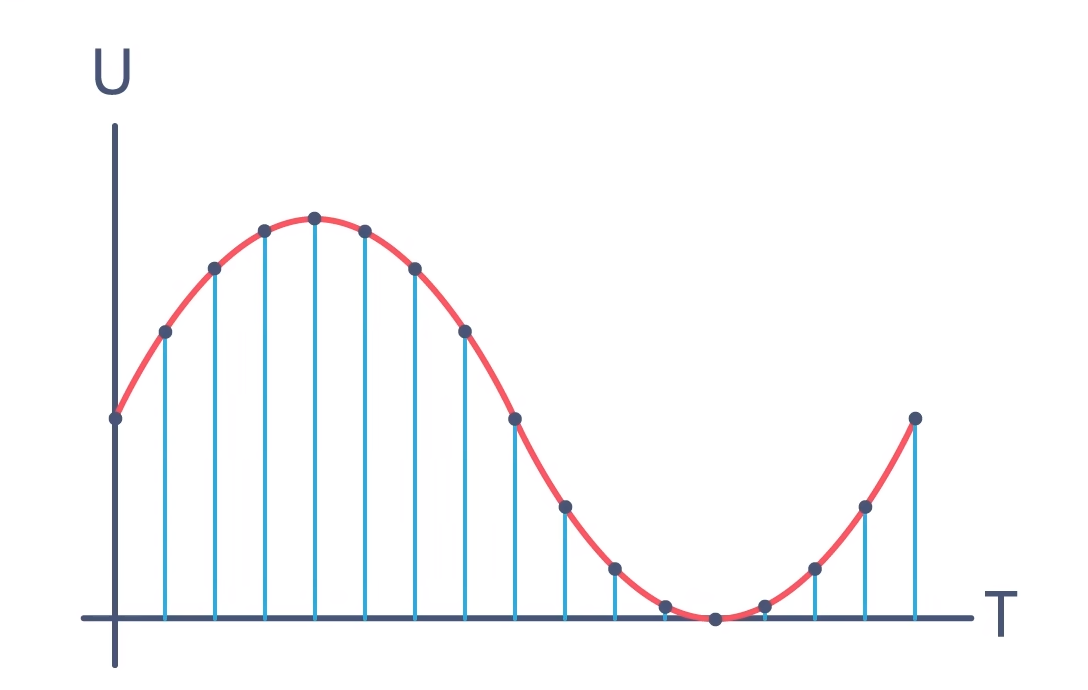固定采样周期
但它还不是数字信号，因为这样的信号在幅值上还是连续的，我们可以称其为抽样信号。这里有一个问题：为什么说信号的幅值仍然是连续的呢？明明它的幅值也已经离散了。这是因为，在每个采样时间点上采集到的模拟信号的精度很高，如果我们能够用数字信号表示这样精度的模拟信号，那么这两种信号之间就没有什么差别了。
抽样信号
2、量化
所以，为了方便信号处理，就需要我们进行下一个数字化步骤：量化。量化就像是分级，比如我们的考试成绩，它可以有各种各样的得分，但考试结果只有A、B、C、D等几类。
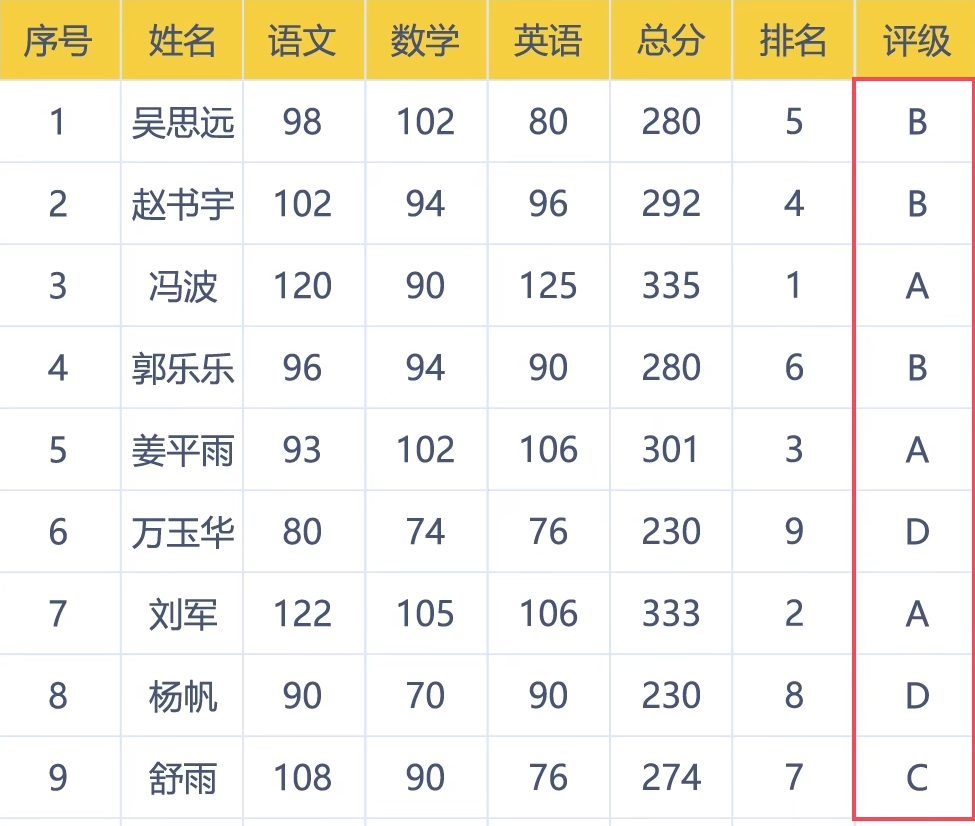
怎么理解呢？我们来举一个具体的例子：某种器件的有效电压是在0至10V，根据规定以0.625V为间隔，将参考电压（10V）分成16份，这样0～0.625V是第一级，0.625～1.25V是第二级，以此类推，我们就可以将10V的参考电压量分成16个级别。其中0.625V是量化间隔，每级量化都是量化间隔的整数倍。比如输入电压是0.3V和0.6V，那么它们经过量化后，都会被归类成第一级，这就是量化的含义。
细心的朋友应该会注意到，这里我们将0.3V和0.6V的电压化为一个等级，这样的量化未免也太粗糙了。虽然量化是为了更加方便的处理数据，但我们还是希望量化后的信号和输入的信号尽量相似，不至于改变原始信号的特性。怎么办？当然是在合理范围内最大程度上减小量化间隔，这样二者之间的差异就很小了。
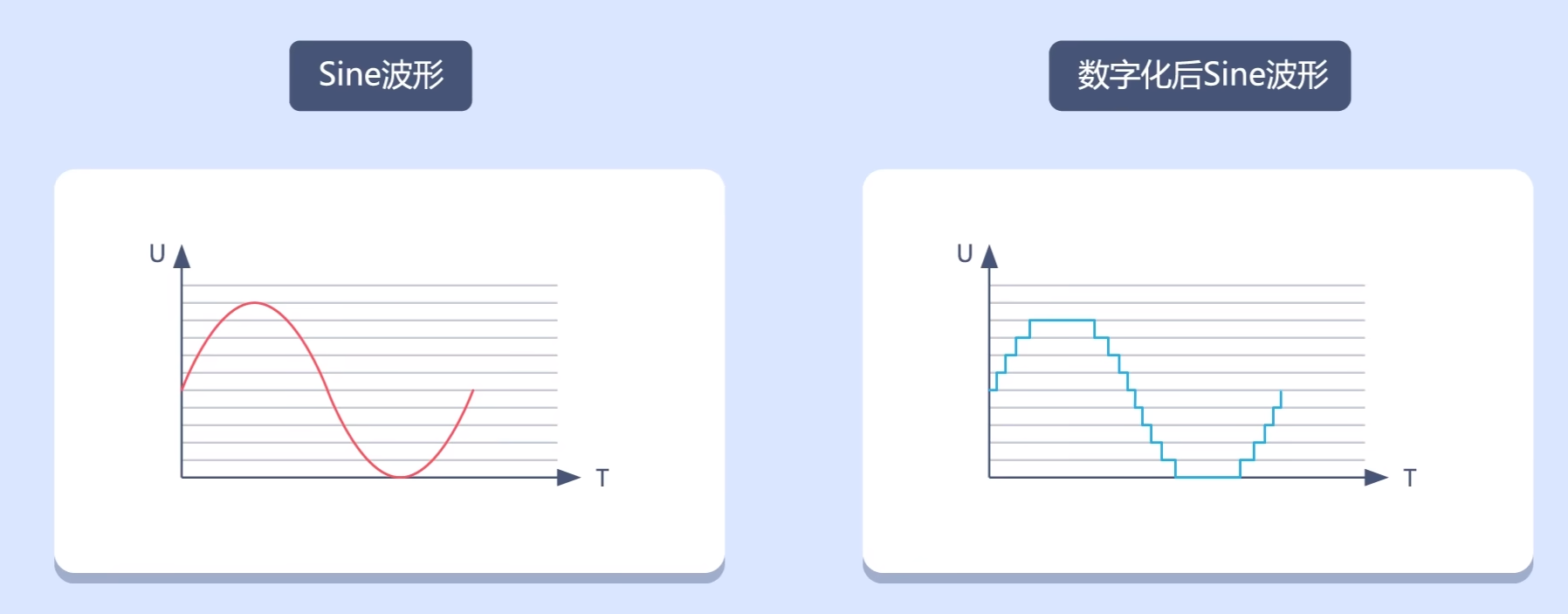量化间隔大
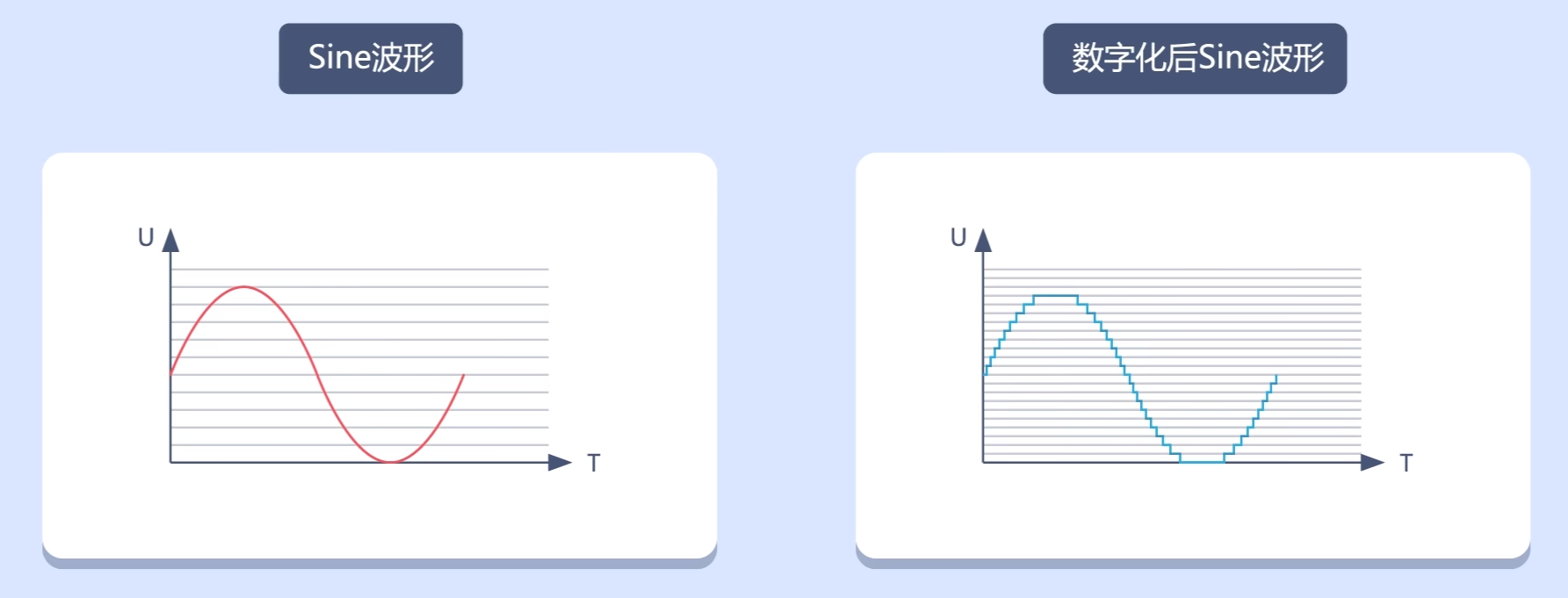量化间隔小
现在我们来做些定义，将量化间隔定义为△，那么量化带来的误差的范围就在正负1/2△之间。而这个误差被称为“量化误差”。
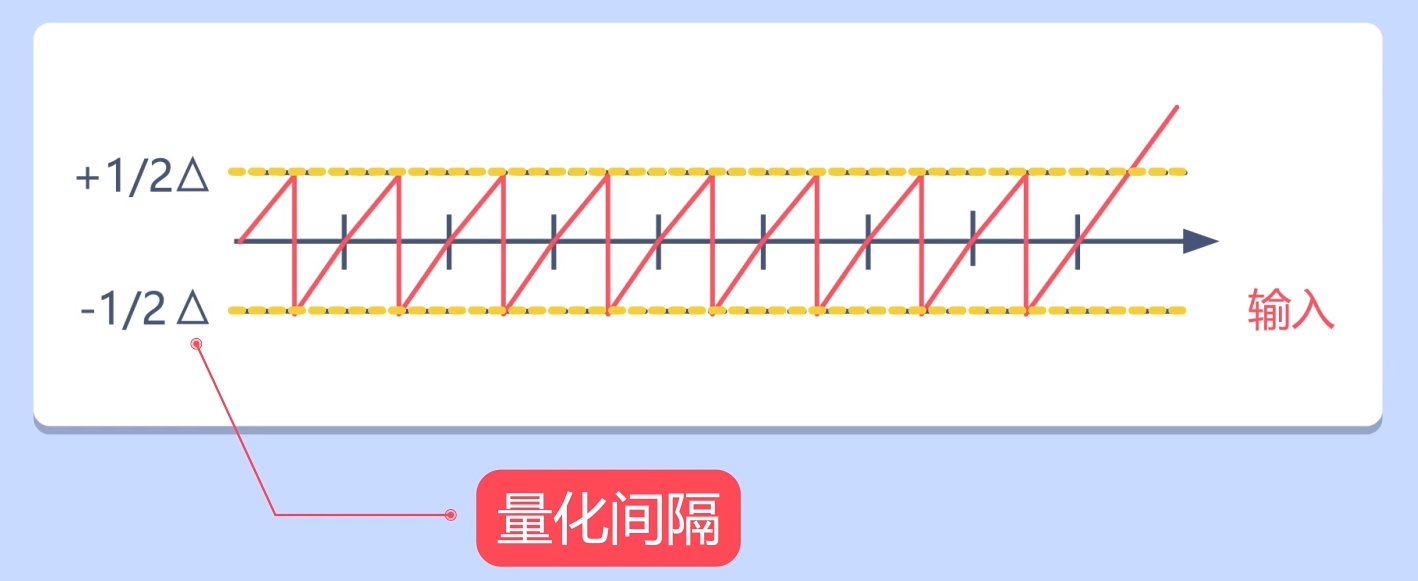
量化间隔越小，量化误差的范围就越小，输入信号与输出信号就越相像，也就是说系统的精度就越高。
量化间隔越小，把额定值分成的份数就越多，也就代表它的分辨率越高。分辨率其实就是系统能够测量的最小变化量，也就是量化间隔。在上述例子中，我们将参考电压分成了16份，是2的4次方，所以它的分辨率为4bit。如果我们将电压分成32份，是2的5次方，那么它的分辨率就是5bit，量化间隔由0.625V变成了0.3125V。
之后我们要讲的几个ADC，都是在通过各种手段减小量化误差，以提高自身的分辨率。具体是怎么做的呢？在之后的内容中将会一一说明，这里暂且按下不表。让我们回到模数转换的步骤中来，经过量化后，模拟信号已经成功数字化，也就是在时间和幅度值上都离散化。下一步就是编码。
3、编码
在之前的例子中我们将参考电压分为了16份，而编码的含义就是用“0”、“1”的组合为每个量化区间编号，以代替相应区间的电压值。案例的分辨率是4bit，那么就需要使用4位的“0”、“1”来为每个量化区间编码。所以，0.3V和0.6V都会被编码为0000。
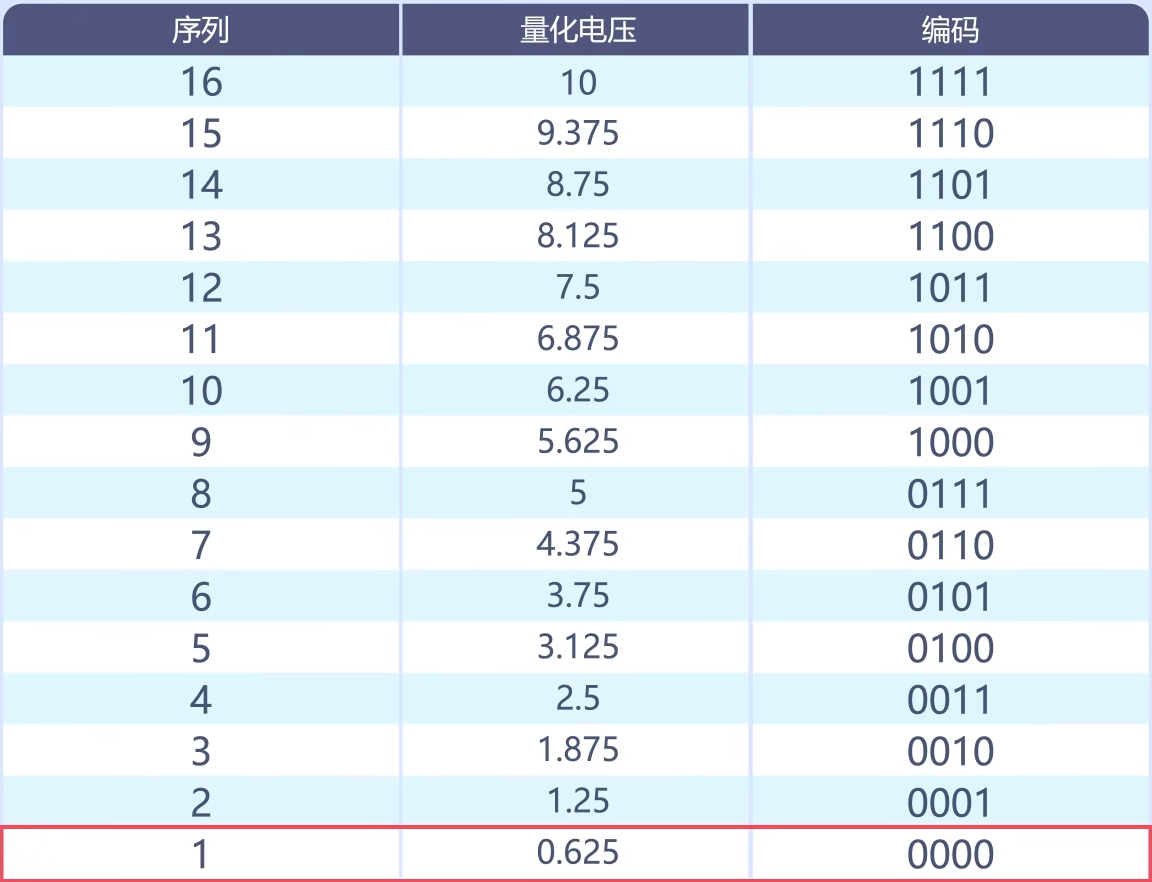
这样模拟信号经过采样，量化，编码后就可以得到一个与其对应的数字信号。
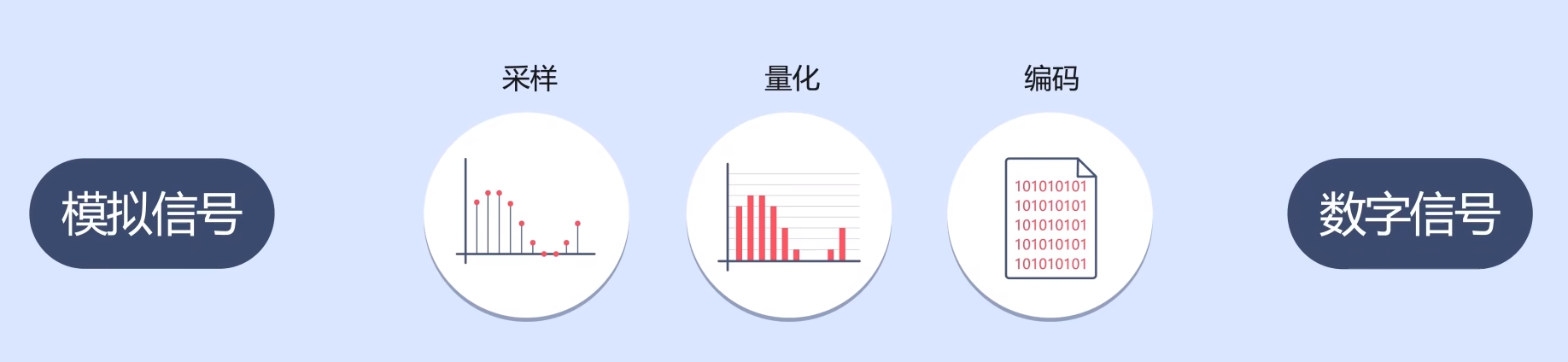
而帮助我们执行这几个步骤的元件就是模数转换器，即ADC。
二、模数转换器(ADC)
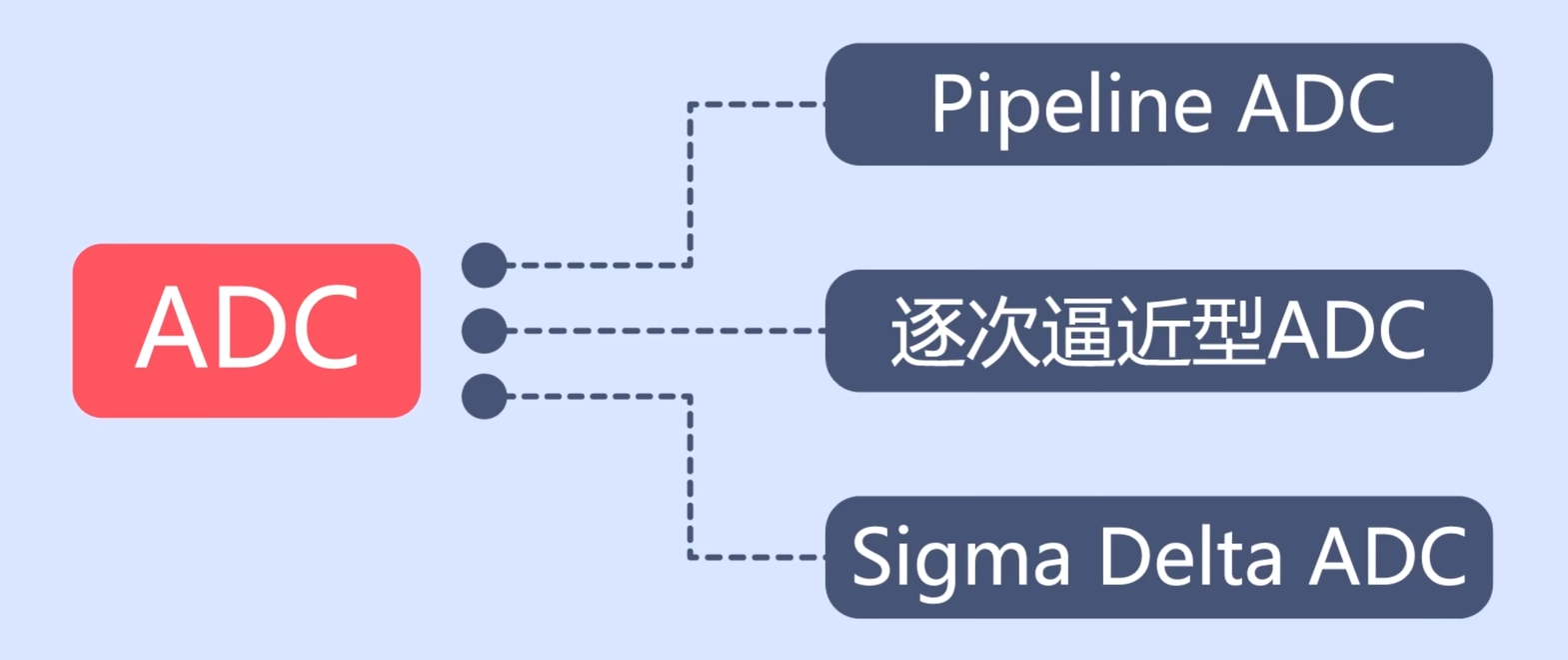几种常见的ADC
1、流水线型(Piepline) ADC
首先要介绍的是Piepline（流水线型）ADC，不过在这之前我们必须先说一说另一种ADC：Flash ADC。因为Piepline ADC就是在Flash ADC的基础上延伸发展而来的。
Flash ADC的基本结构是这样的：
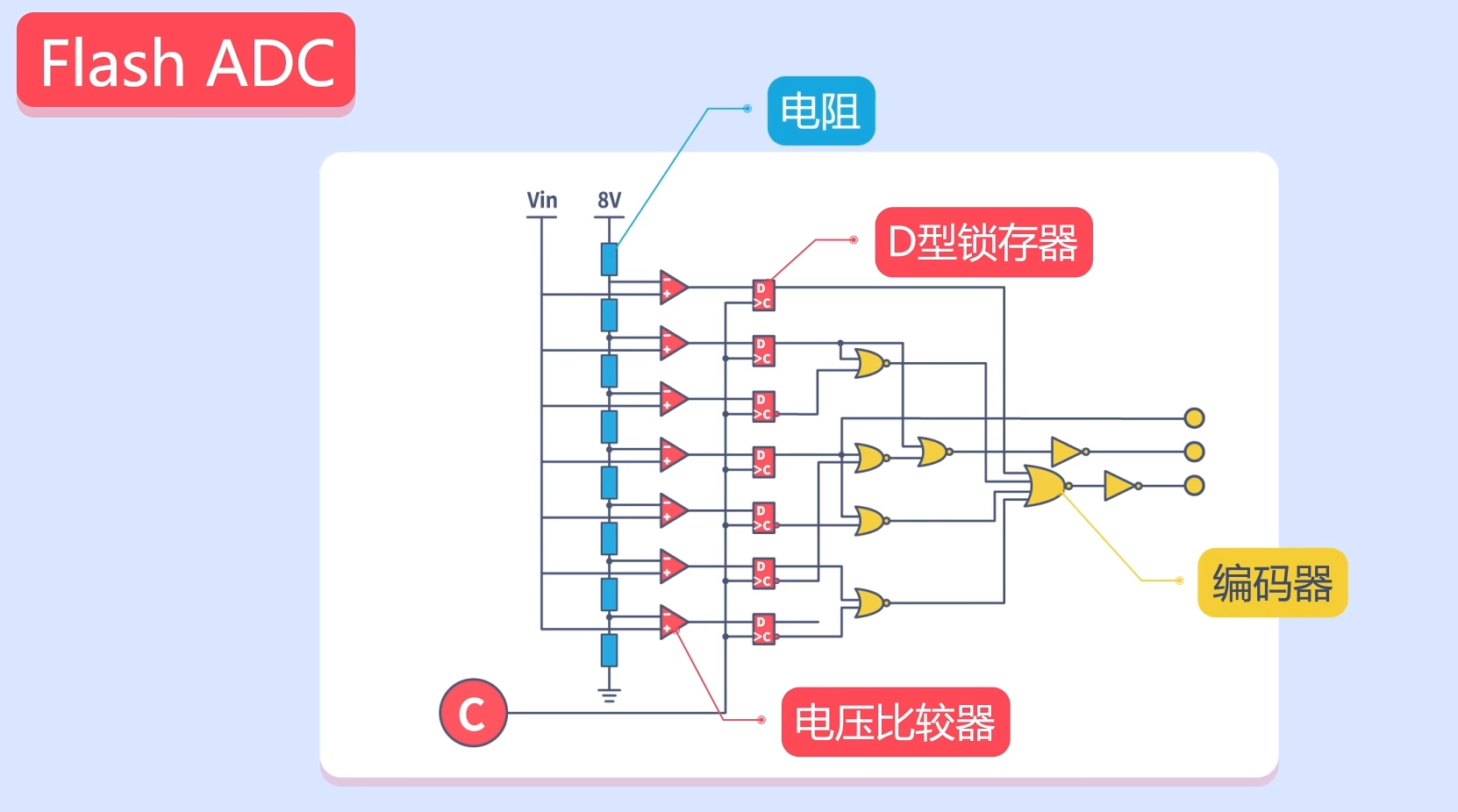
它由电阻，电压比较器、D型锁存器，以及编码器构成。图中所示的是一个3bit的Flash ADC。它将8V的参考电压通过8个相同的电阻分为8份（23）。其运行过程是这样的，假设经过一个时钟的采样周期，采集到的模拟电压是3.5V，此电压会与每一级的量化电压比较，如果超出量化电压就输出1，反之则输出0。
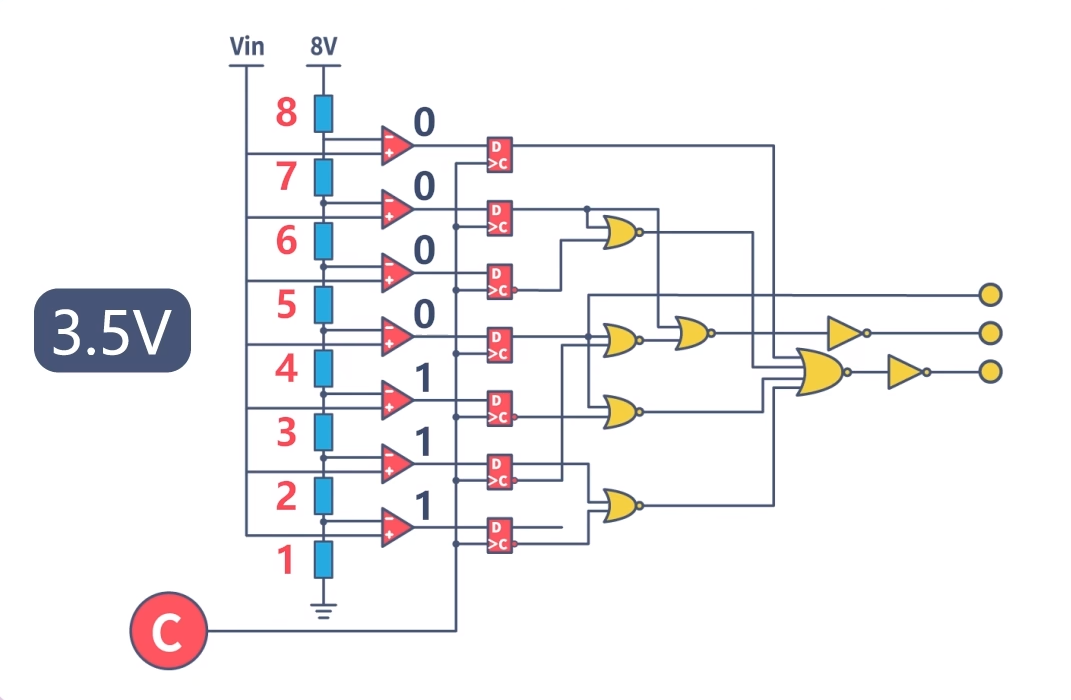
这样电压比较器就输出0000111的电平信号，这些电平信号会保存在D触发器中，只要C端的信号不改变，触发器内的信号信息就不会改变。最后通过编码器将触发器内的信号，编码成数字信号输出。
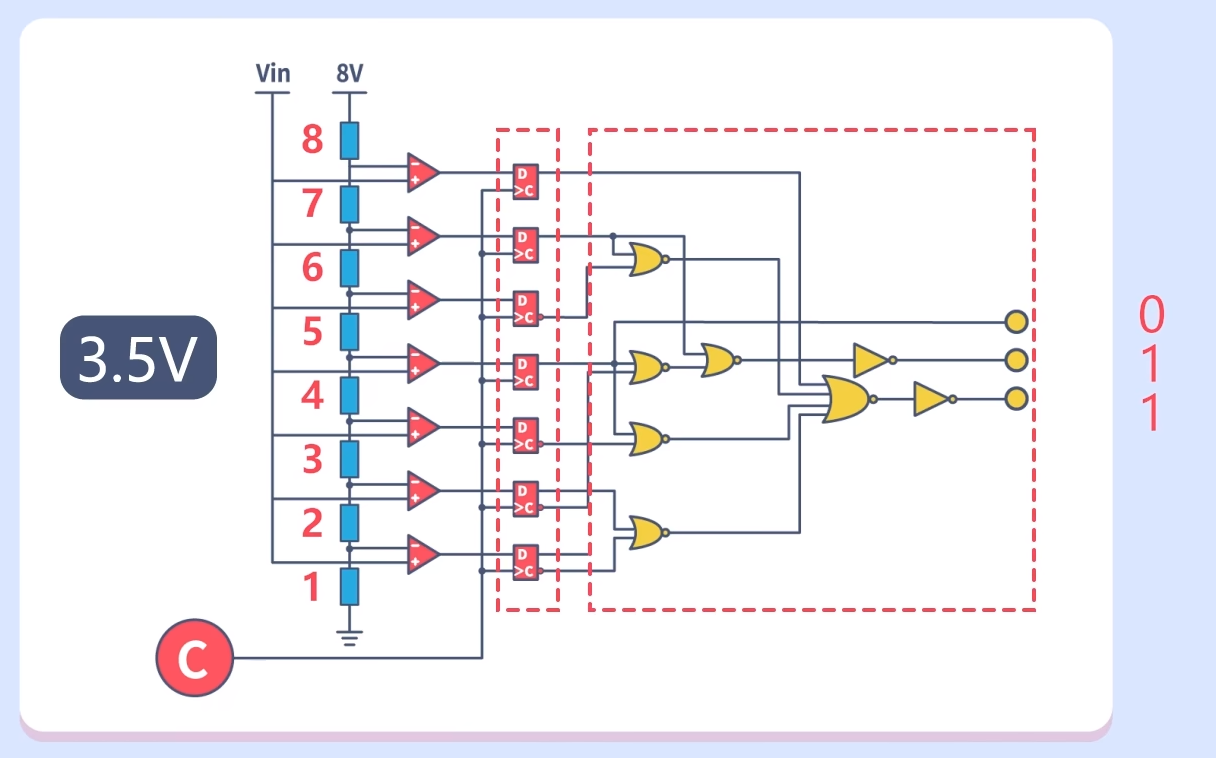
电路结构中的D触发器和RS触发器有些类似，都可以用来储存信号。当C端的信号是0，触发器内的信息不允许改变，如果C端信号变为1，则触发器内的信息可以变化。观察整个电路结构可以发现，Flash ADC的转化速率无疑是很高的，基本只需要1个时钟周期。之后的比较、锁存等步骤用时可以很短。但它的缺点是分辨率低，只有3bit。也就是说，只有电压的变化超过1V，Flash ADC才会对其使用不同的编码。具体编码如下图：
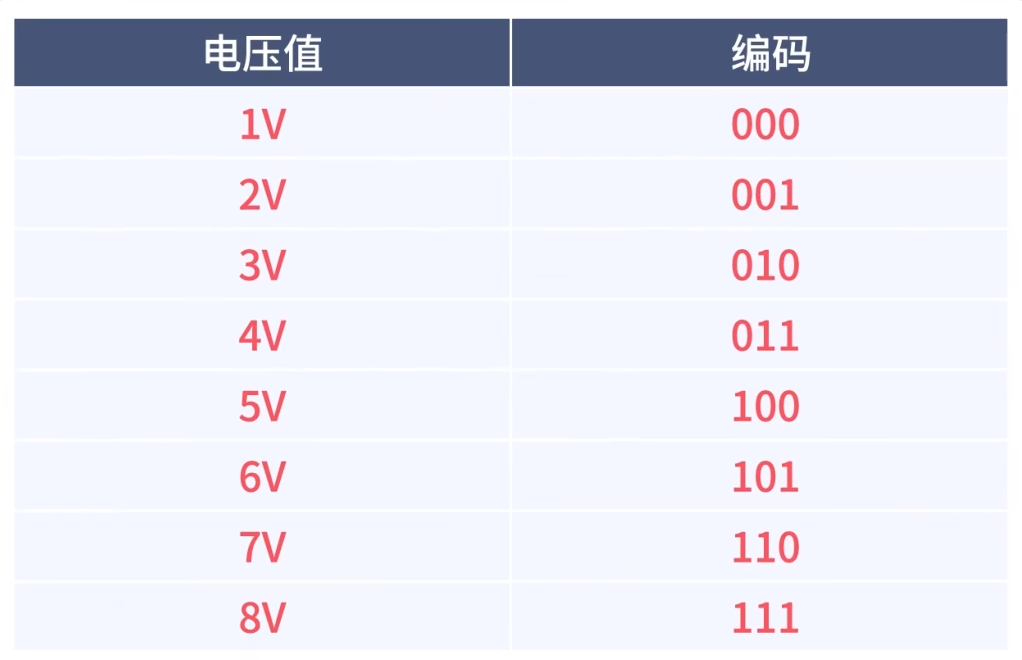
如果我们想要减小量化间隔，提高分辨率，那么电路所需要的比较器，锁存器等元件将成指数级上升（2n-1）。比如要将分辨率提高到16bit，那么就需要65535个比较器。这就一定会出现芯片面积大，功耗高等问题。所以这样的ADC适用于低分辨率，但需要快速响应的场合中。
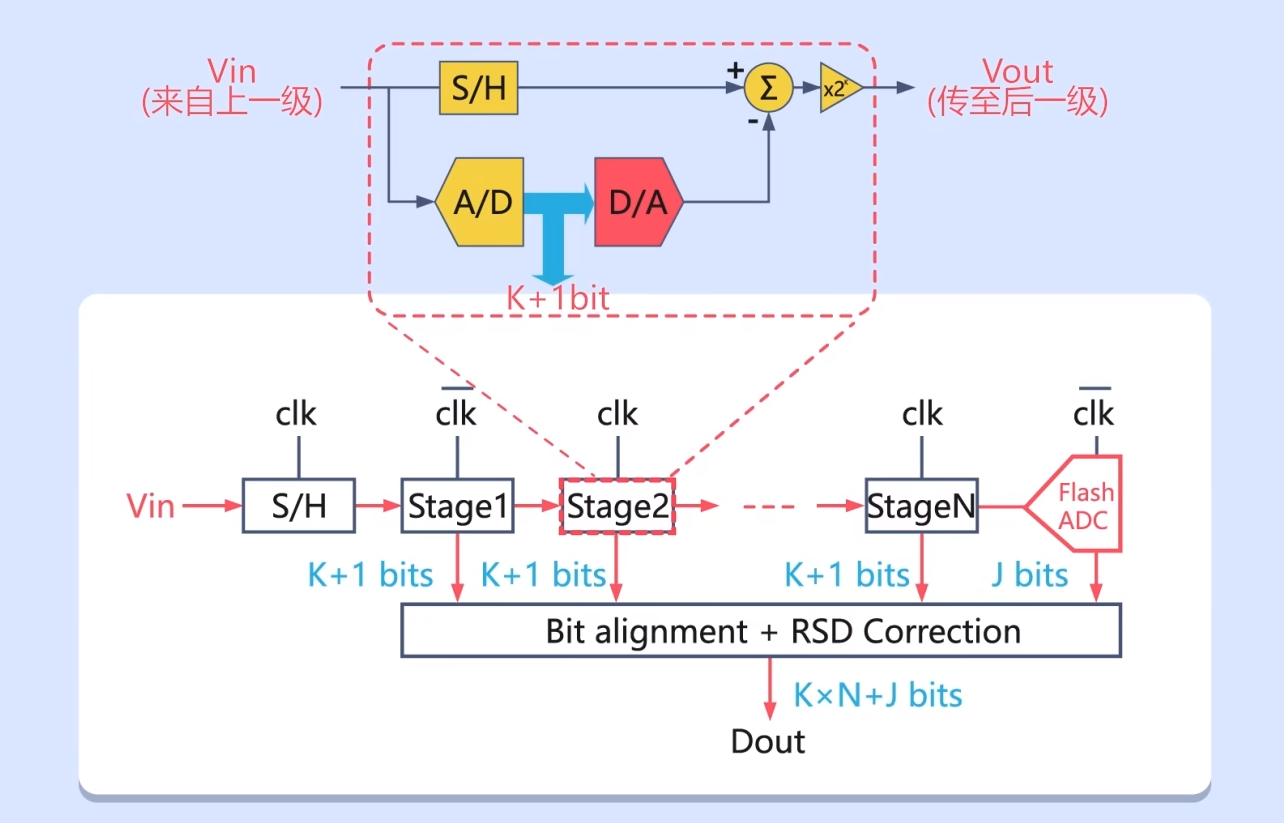
为了解决Flash ADC的问题，流水线型ADC（Piepline ADC）便应运而生。这是一个1.5bit流水线ADC的结构示意图：
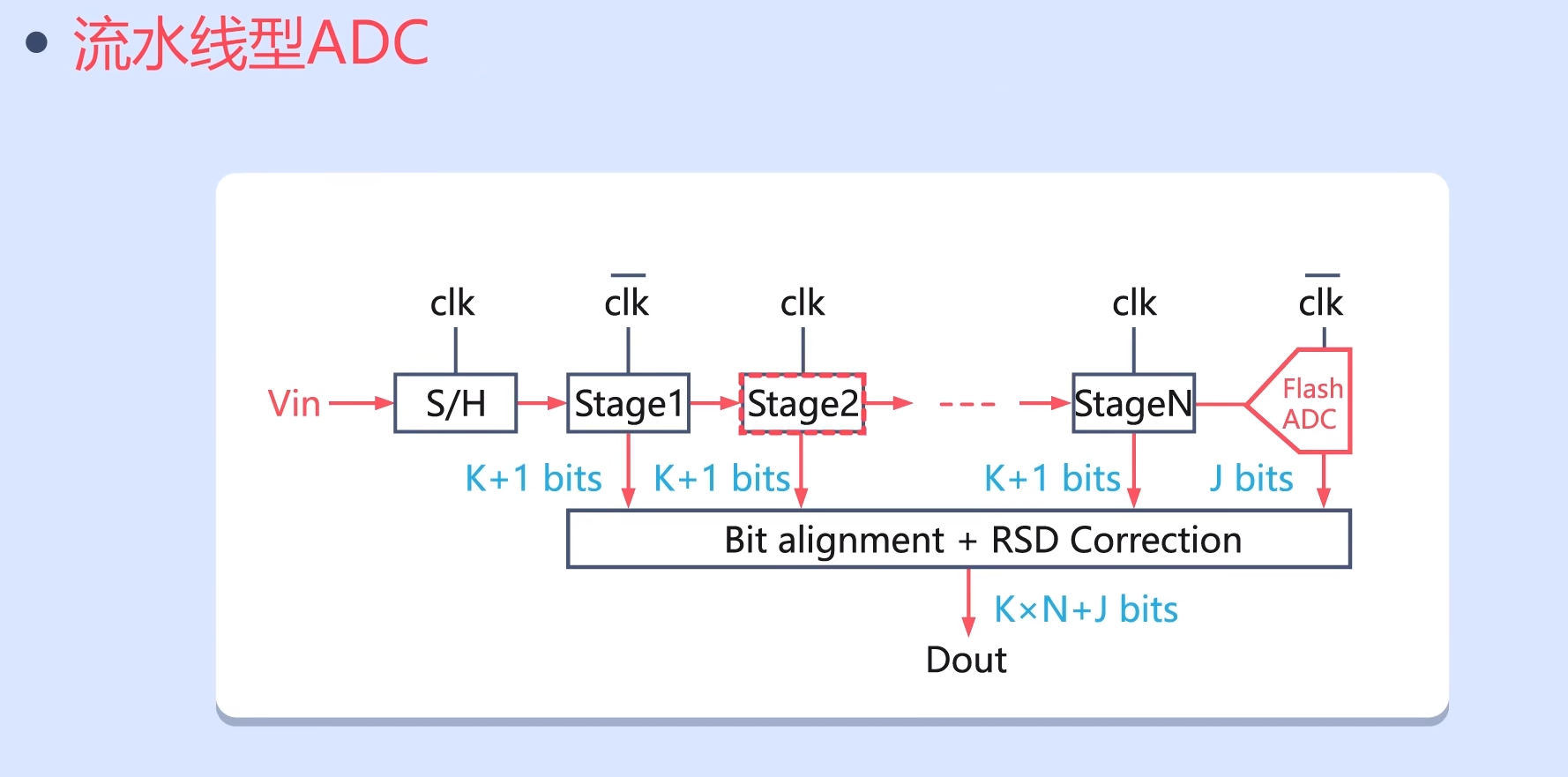
当经过采样的模拟电压输入（Vin）后，会经过N个Stage，最后再通过一个Flash ADC。整个过程就像流水线上的商品一样，经过一级一级的加工，最终完成生产，所以称其为流水线型ADC。以1.5bit流水线型ADC为例，我们来看看其中最重要的Stage单元是如何运行的。当上一级的电压信号进入时，首先要进行一次A/D转换，这次转换的分辨率是1bit，也就是说只用到1个电压比较器。
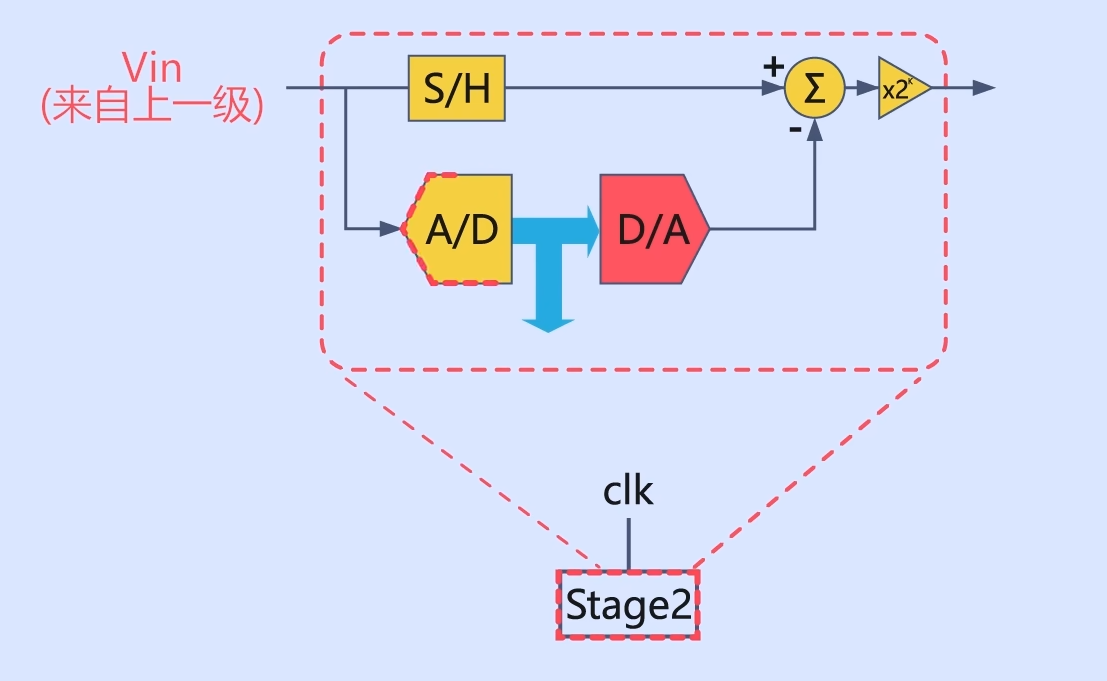
输出相应数据后，在进行一次D/A转换，将其变回到模拟信号。
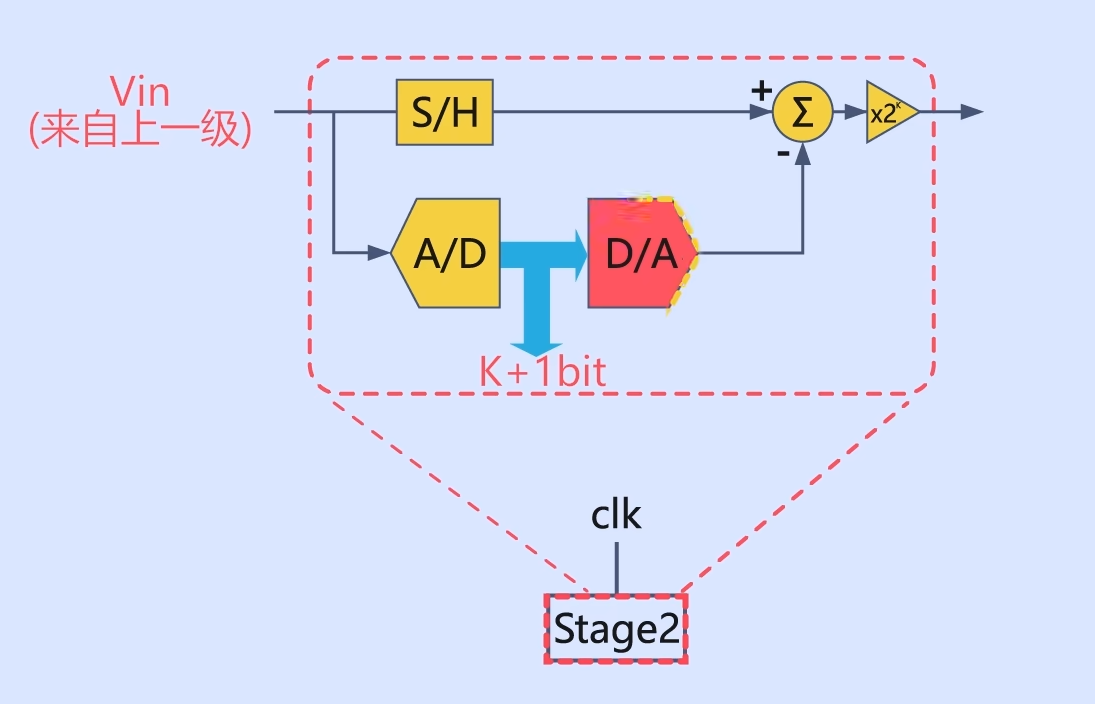
然后用原来的模拟信号减去转换后的的模拟信号，将最终结果乘以二后再传递至下一级Stage。
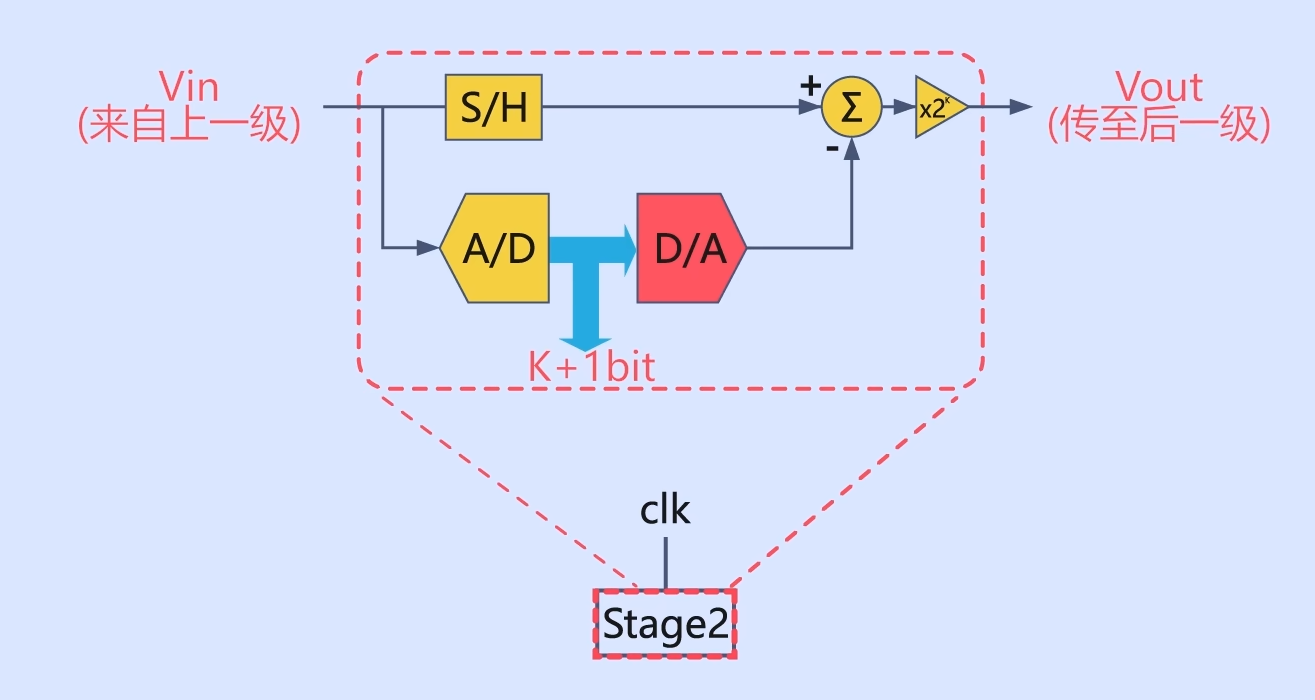
如此这般重复，就可以完成数字信号的转换了。
我们来看一个具体的实例，对这个转换过程可能会更加清楚一些。但在这个例子中我们没有以1.5bit流水线型ADC举例，因为1.5bit流水线型ADC考虑了误差因素，转换相对来说要更复杂一些。而这个实例子是一个具有4bit分辨率的1bit流水线型ADC。
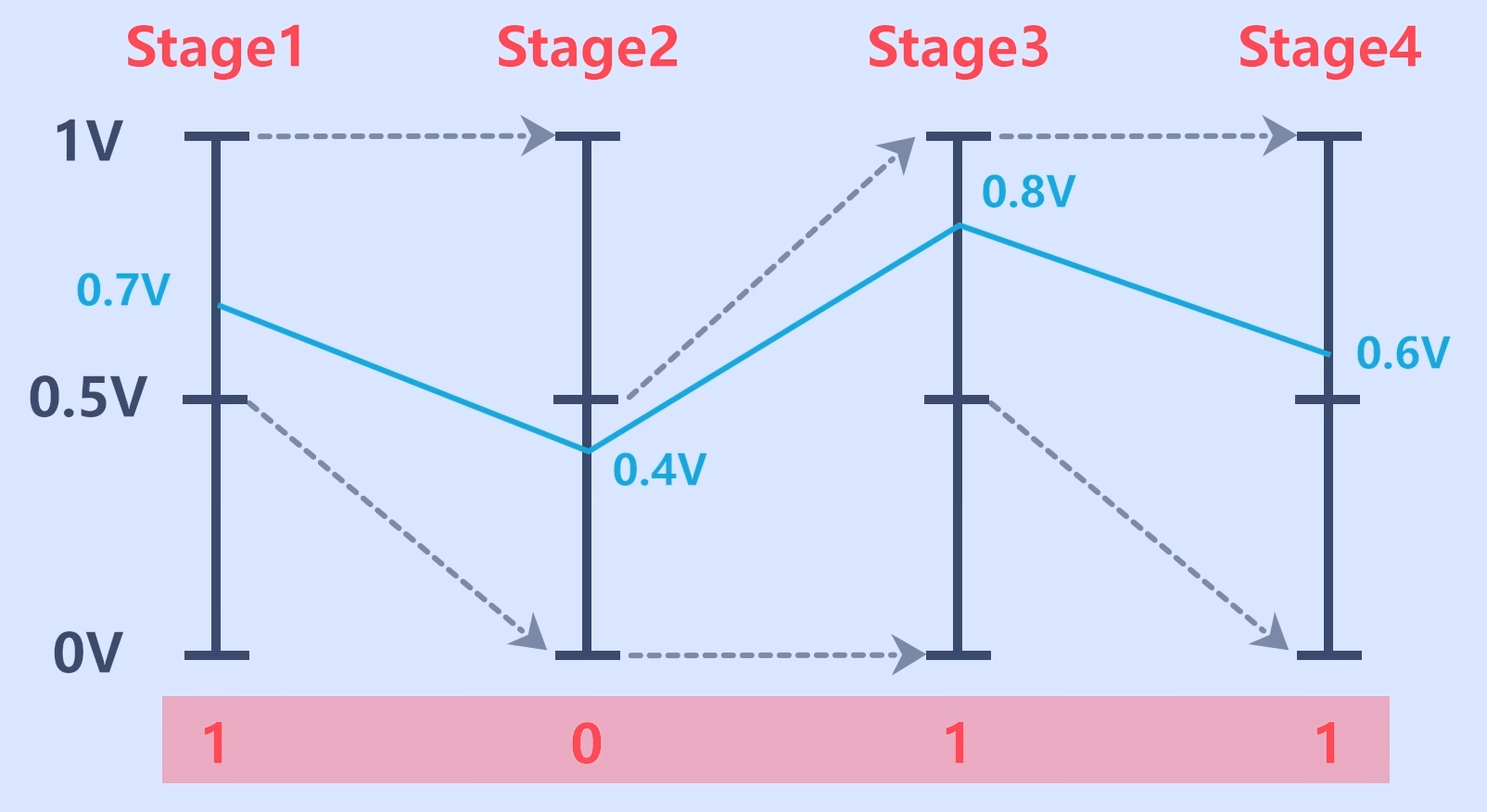
假设参考电压是1V，每级Stage的分辨率是1bit，所以电压在0～0.5V时输出0，在0.5～1V时输出1。当输入的电压是0.7V，Stage1输出1；用0.7V减去0.5V后乘以2后的结果0.4V输入到Stage2，输出0；将原始电压0.4V乘以2后的0.8V输入到Stage3中，输出1；将0.8V减去0.5V后乘以2的结果0.6V，输入到Stage4，输出1，这样就实现了4bit的分辨率，最后输出的结果是1011。大家如果有兴趣可以用4bit Flash ADC的方式，列出其真值表看一看，0.7V电压的编码正是1011。而且4bit Flash ADC需要用到16个比较器，而流水线ADC只需要4个比较器。分辨率越高，节省的硬件资源就越多。
流水线型ADC的采样速度快，同时功耗也比较低，但它对电路工艺要求很高，电路较为复杂。在无线通信、数字视频等领域应用广泛。
2、逐次逼近型(SAR)ADC
接下来要介绍的是逐次逼近型（SAR）ADC。
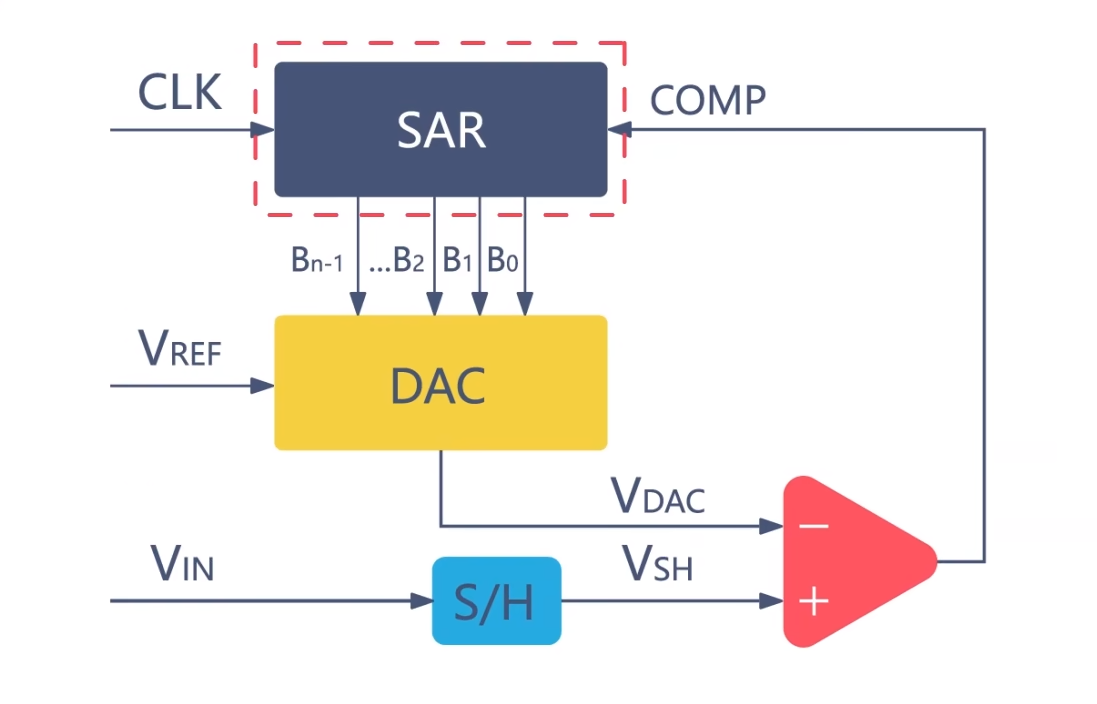
它使用了一种二分搜索算法实现数字信号的转换。我们结合一个具体实例为大家介绍这种算法。
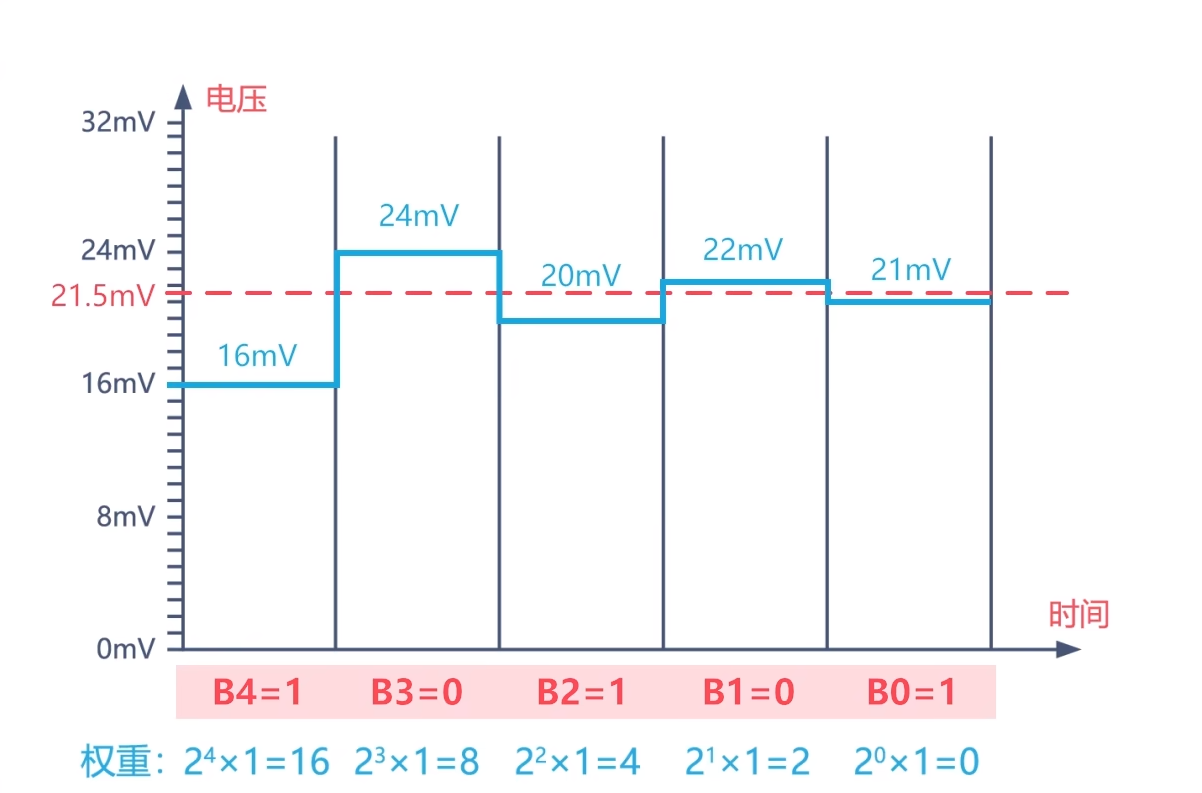二分搜索算法示例
如图所示，这是一个5bit分辨率的SAR ADC，其参考电压（Vref）是32mV，这样它的最小量化电压（ΔV）就是1毫伏（32/25）。当我们输入的电压是21.5mV时，ADC首先用参考电压的一半也就是½Vref与输入电压比较:21.5>16所以首位输出1；第二次比较时，用½Vref+¼Vref之和，也就是24mV与输入电压比较：21.5<24，所以第二位输出0，意思就是前两位相加的权重较大，所以舍去第二位；第三次比较时，用½Vref+1/8Vref之和，也就是20mV与输入电压比较：21.5>20，所以第三位输出1，意思是第一位与第三位的权重相加小于输入电压，所以保留第三位；第四次比较时，用½Vref+1/8Vref+1/16Vref之和，也就是22mV与输入电压比较：21.5<22，所以第四位输出0，那么就舍去第四位；第五次比较时，用½Vref+1/8Vref+1/32Vref之和，也就是21mV与输入电压比较：21.5>21，所以第五位输出1，意思是保留第五位。这样SAR ADC最后输出的结果就是10101。
SAR ADC能够执行二分搜索算法，是因为其电路结构中的逐次逼近（SAR）寄存器。
电路中的DAC模块是数模转换器，负责将数字信号转换为模拟信号。
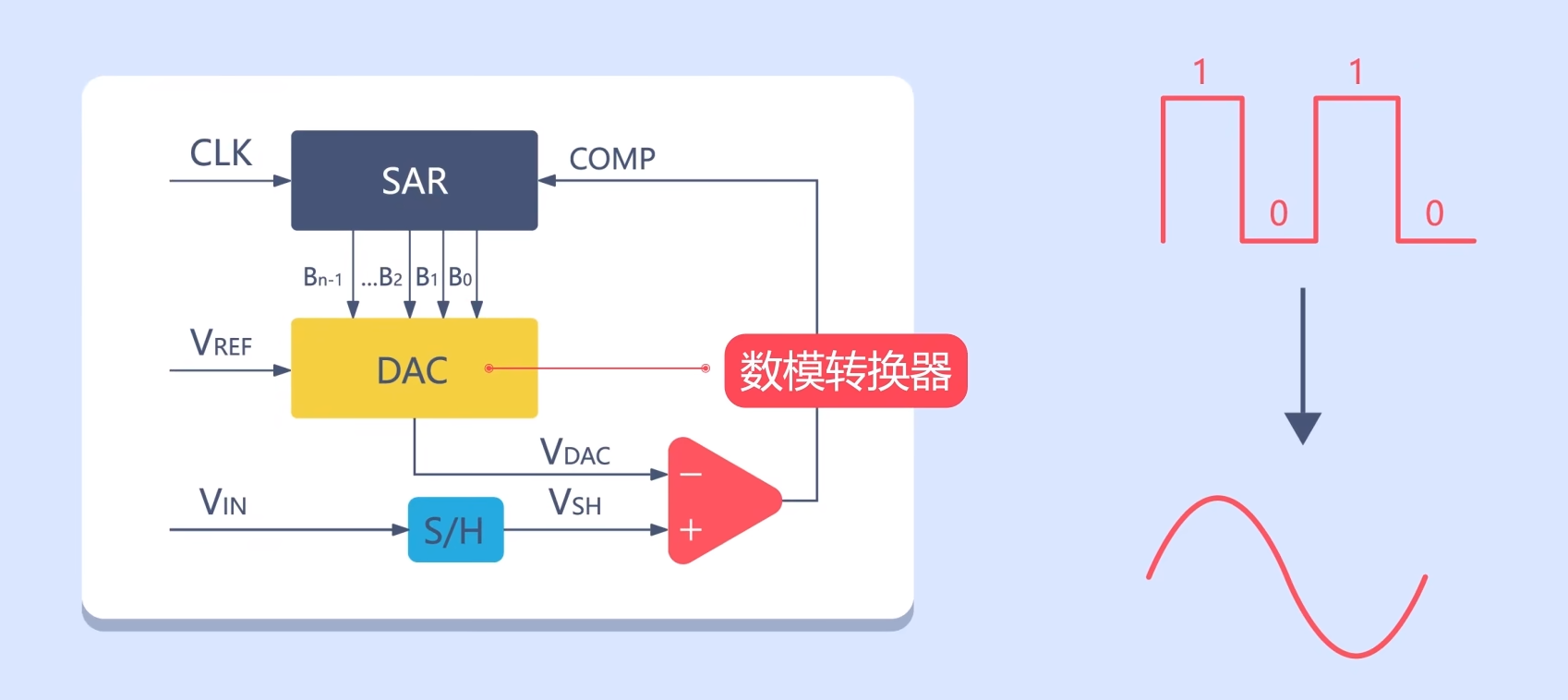
通过不断的循环比较，SAR ADC达到了既节省资源，又能提高自身分辨率的目的。
逐次比较型ADC具有中高的转换精度和速度，功耗较低，但它的设计复杂，生产成本高。这种ADC的应用范围很广，在工业控制，信号采集等方面都有应用。
3、Σ-Δ(Delta Sigma)ADC
最后要介绍Σ-Δ(Delta Sigma)ADC。其结构如图所示：
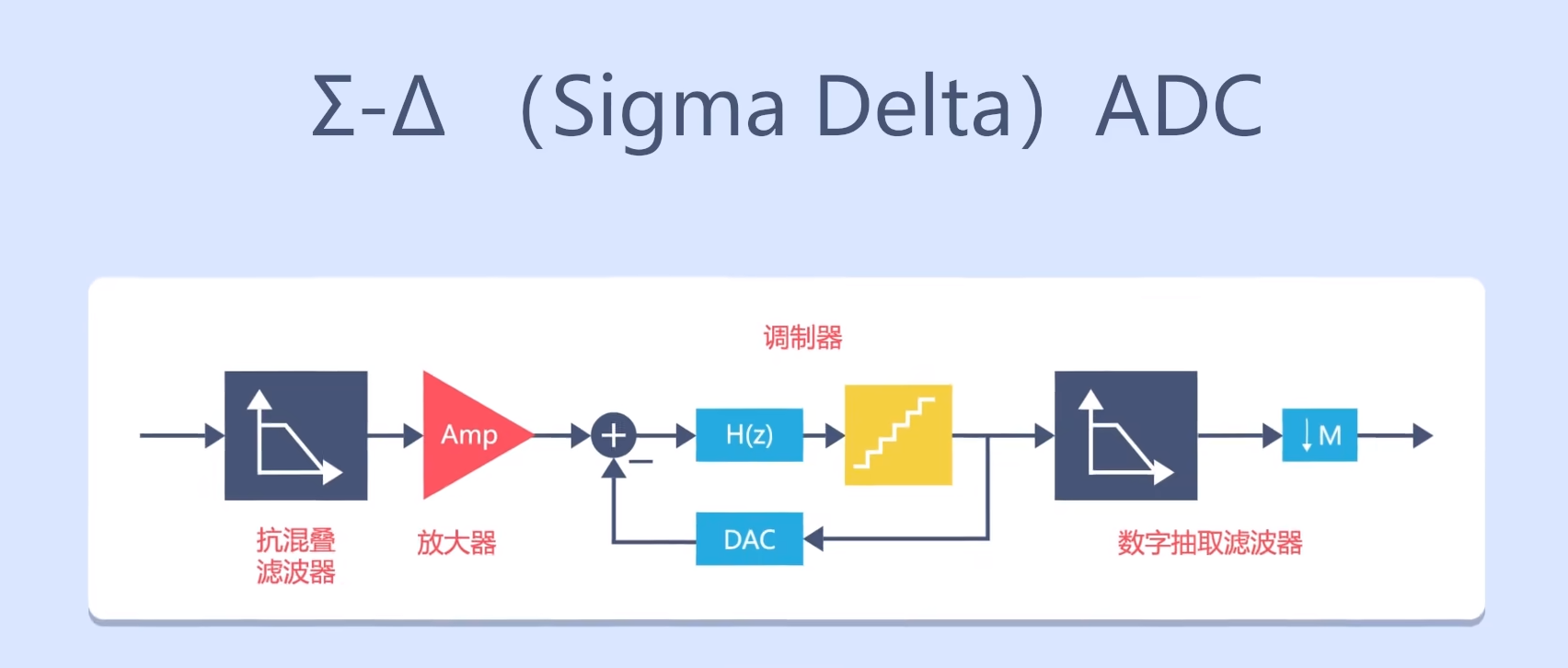
输入信号首先要经过一个抗混叠滤波器，将信号的高频噪声过滤掉。
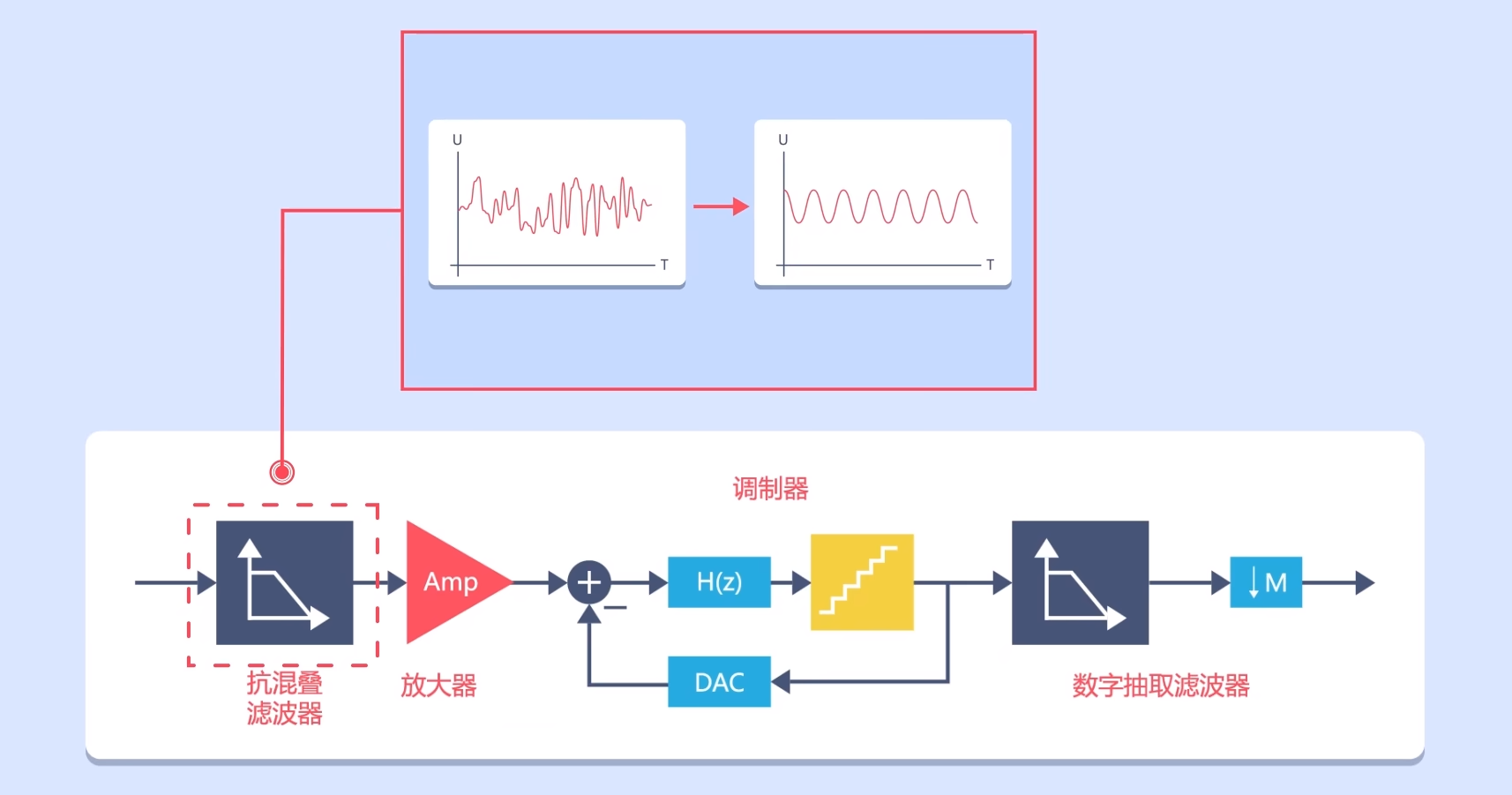
然后通过放大器将信号放大或衰减成合适调制器量程的信号，以免造成误差。
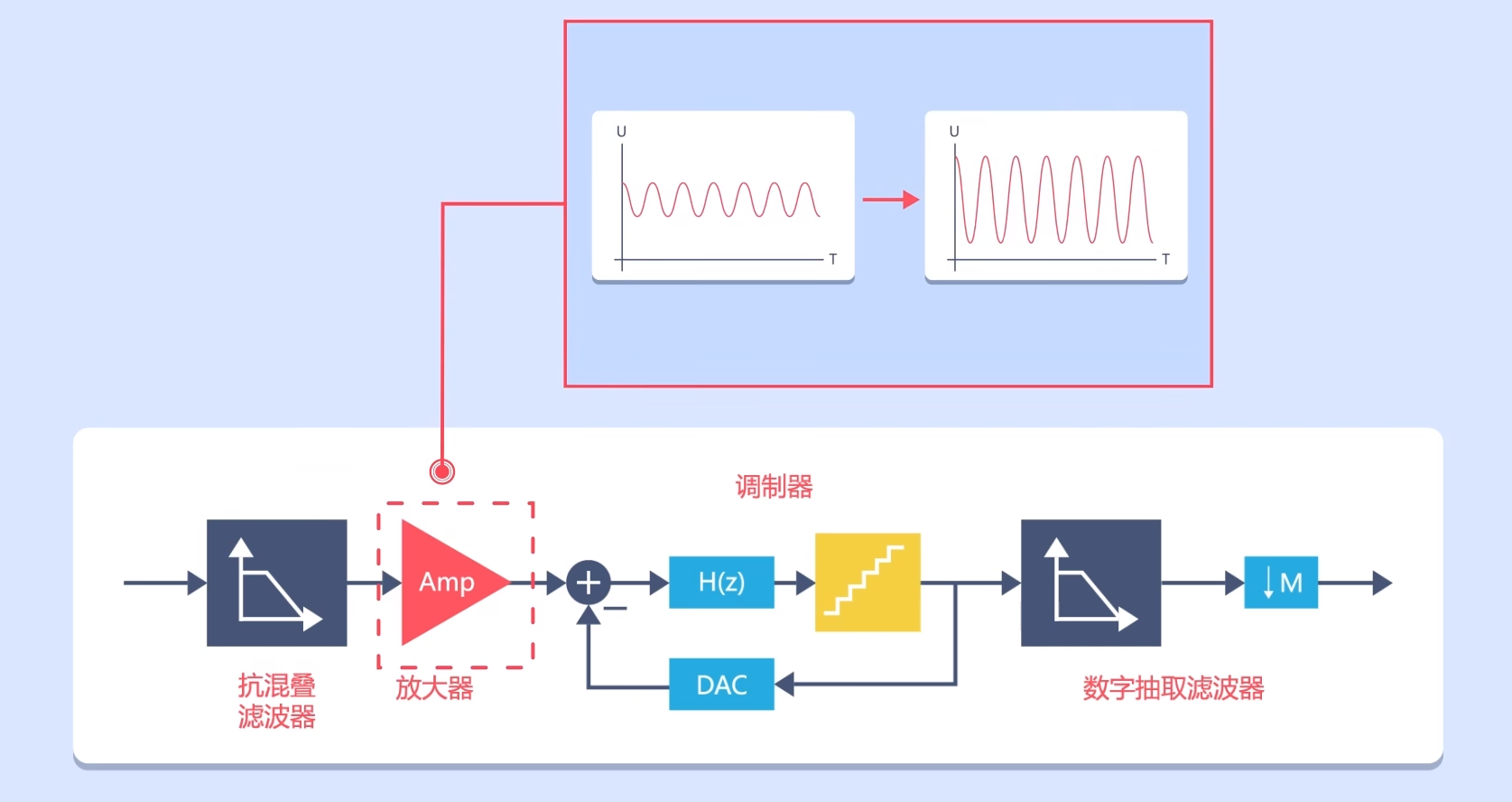
调理后的信号会进入调制器中，经过调制器调制，输入的模拟信号会变成类似于PWM信号由时间参数表征信息的信号。
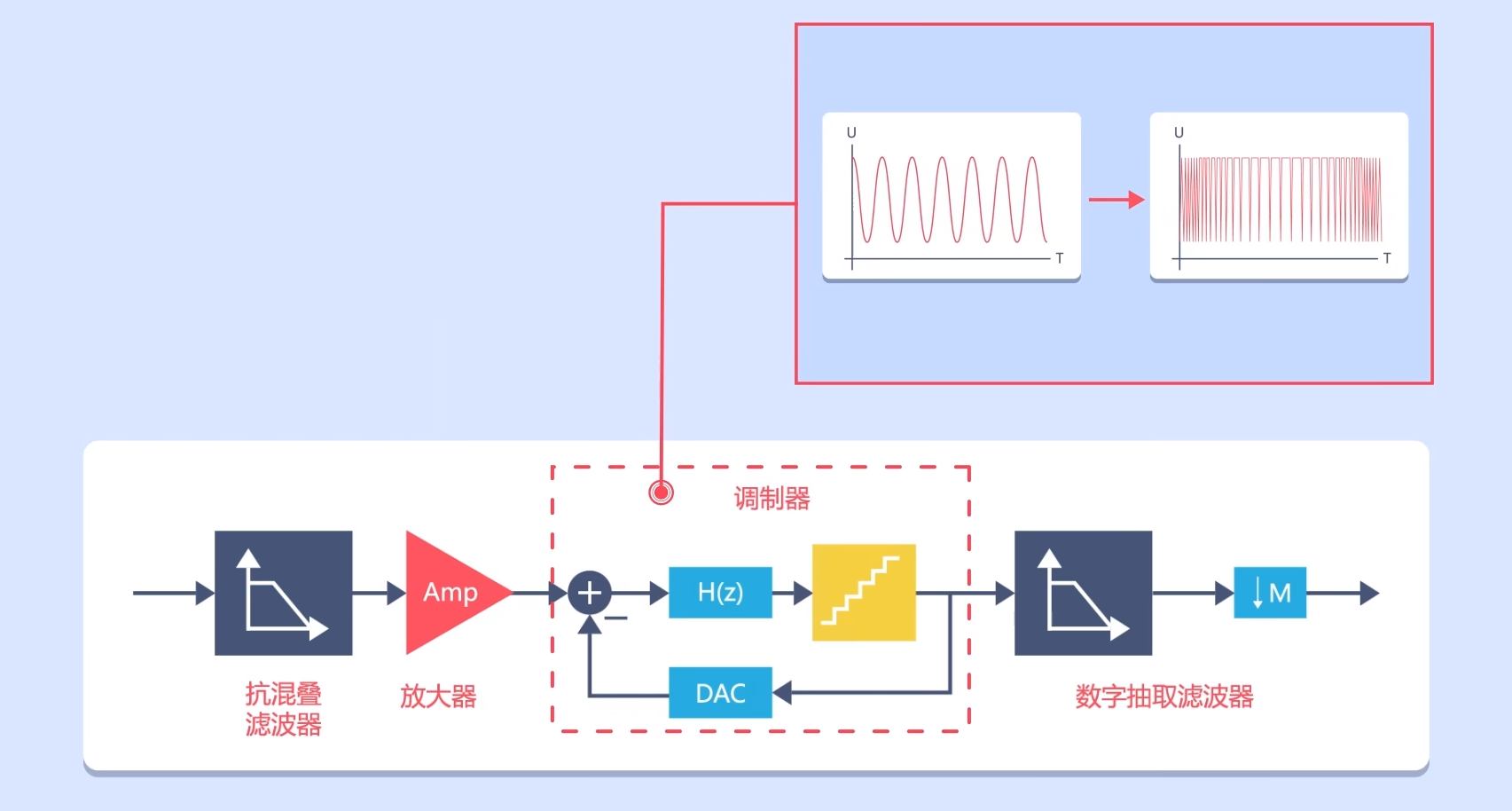
然后再将它输入到数字抽取滤波器中进行滤波抽样等处理，就可以得到数字信号了。
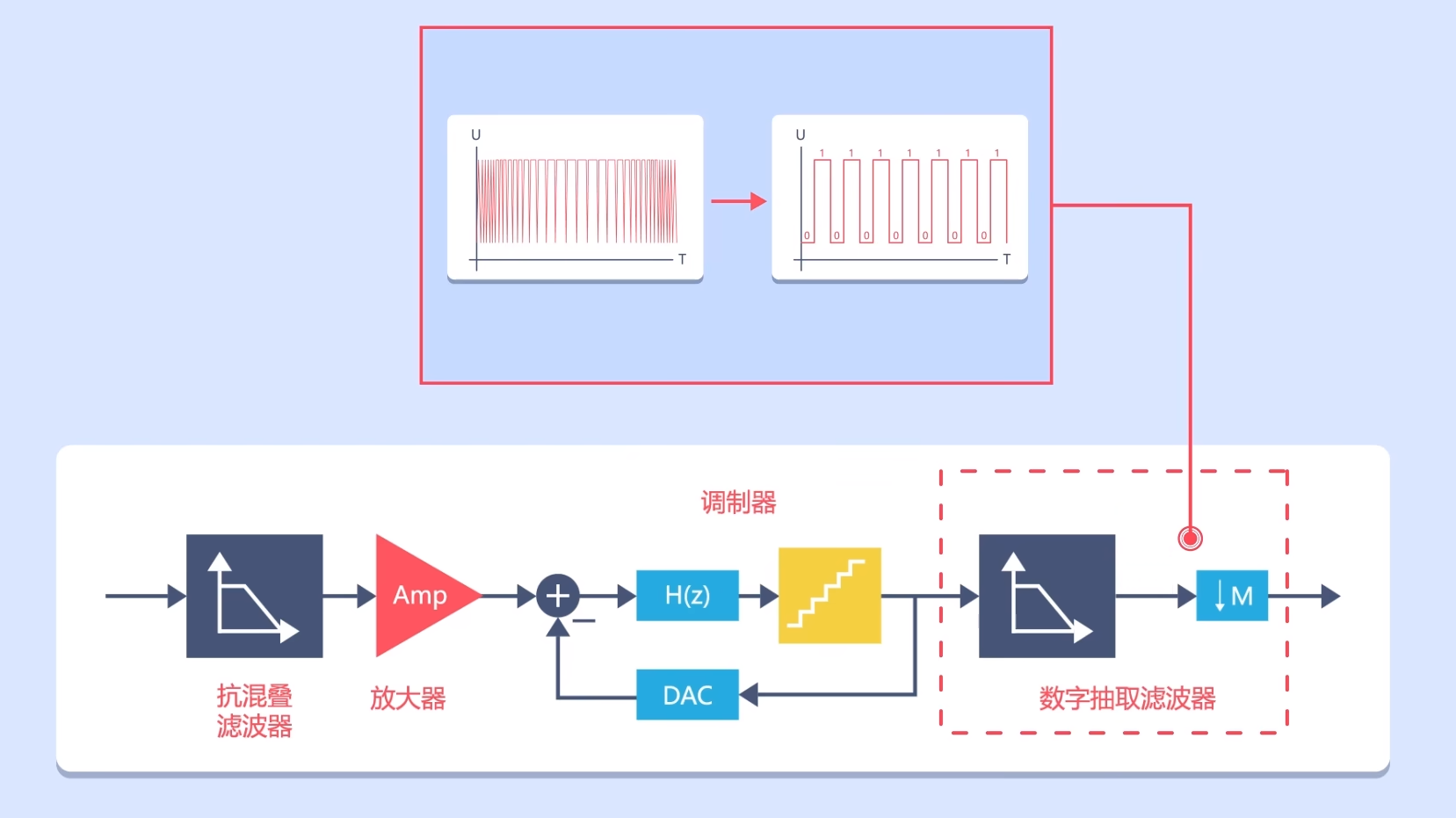
在Σ-ΔADC中调制器和数字抽取滤波器是很重要的两部分内容。这里我们着重介绍Σ-Δ调制器，因为它与ADC能够达到的分辨率息息相关。其具体电路结构如图所示：由积分器、ADC、DAC等组成。
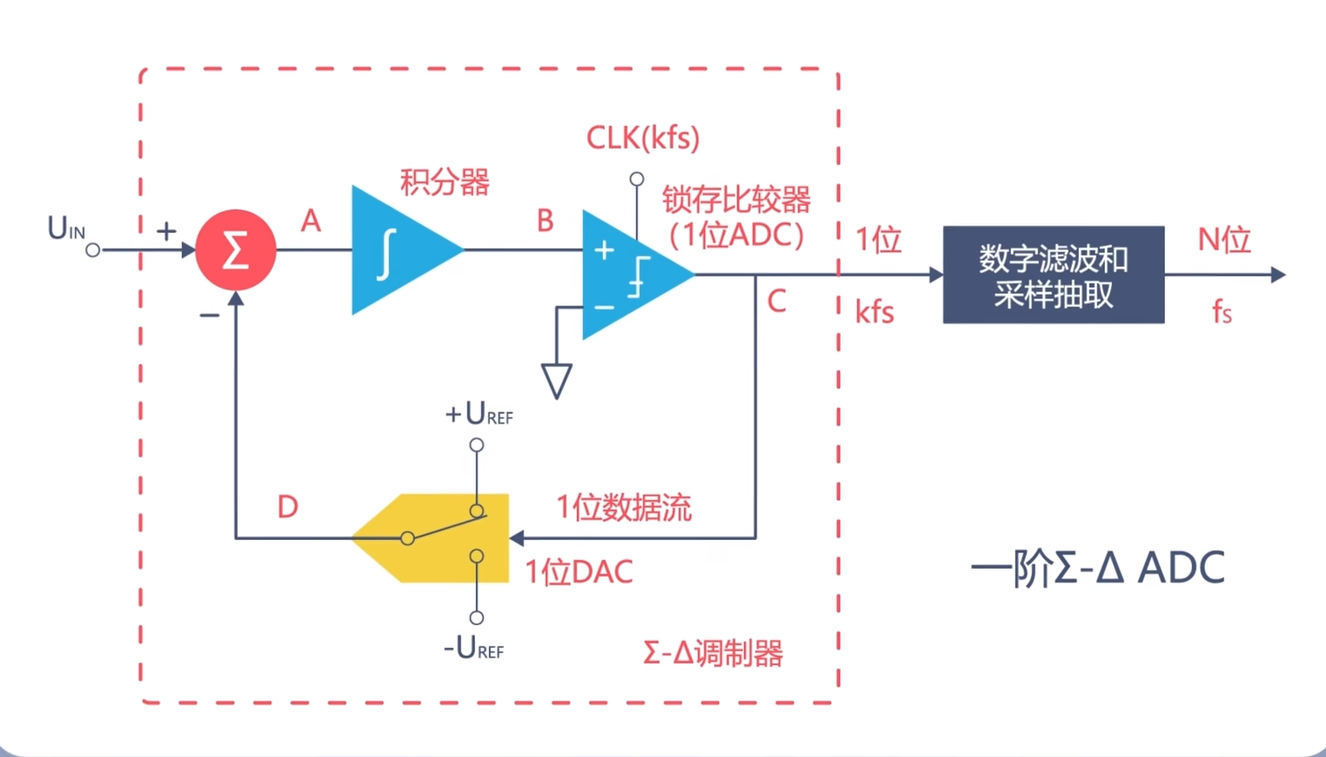
这是一个一阶Σ-ΔADC，还有二阶甚至是更多阶数的Σ-ΔADC。
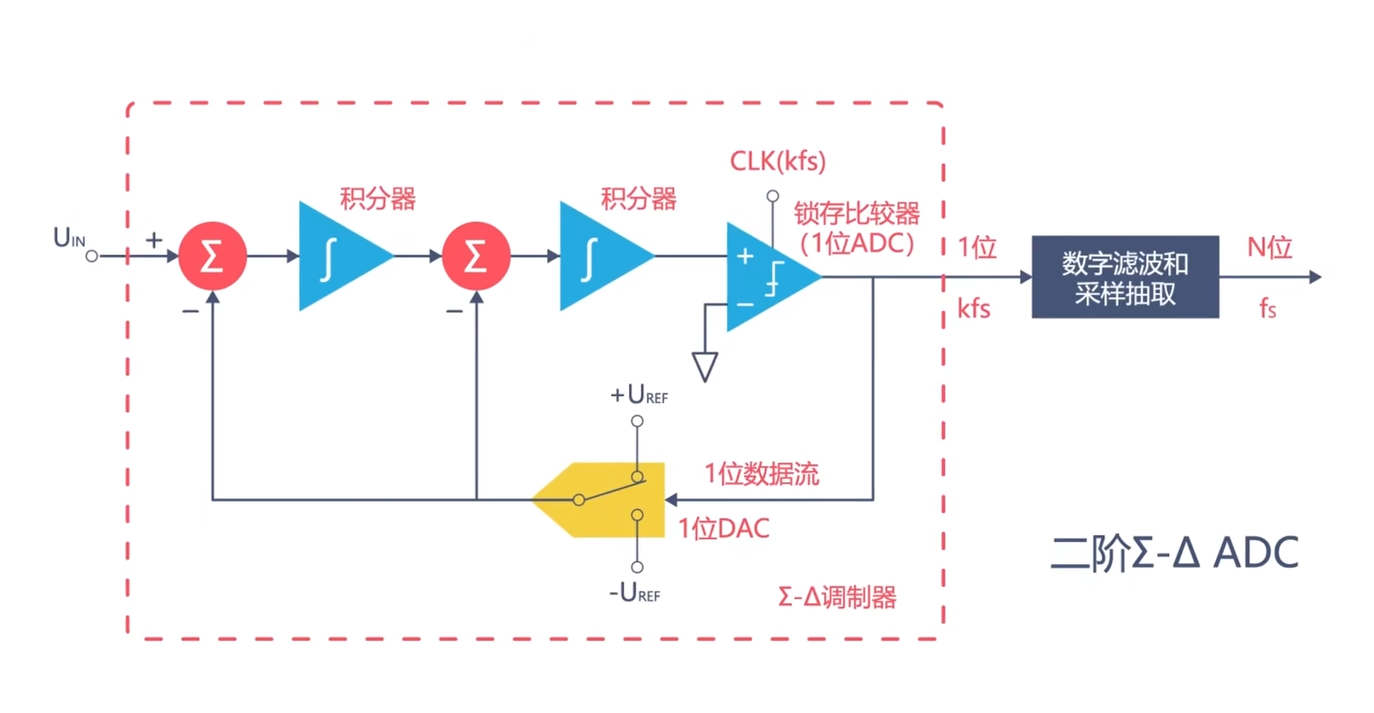
阶数越多，Σ-ΔADC能够达到的分辨率也就越高。最高可以达到24-bit，也就是说它可以将额定量程分成16777216份。怎么做到的呢？我们将输出信号转换到频域中可以发现，在理想状态下，输出信号只由输入信号和量化噪声组成。
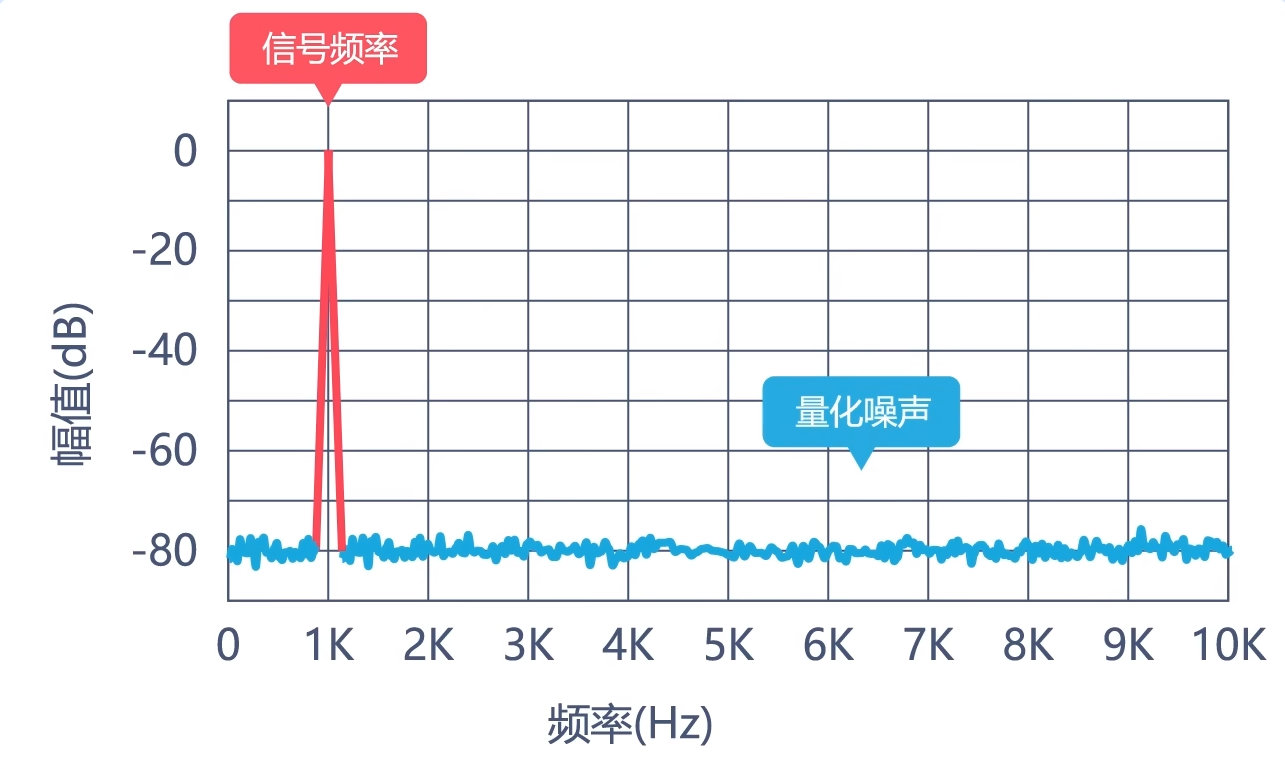
这里的量化噪声是由量化时的量化误差转换而来。那么Σ-Δ调制器就运用过采样和噪声整形技术去抑制信号中的量化噪声，这也就相当于减小了量化误差，从而达到提高ADC分辨率的目的。
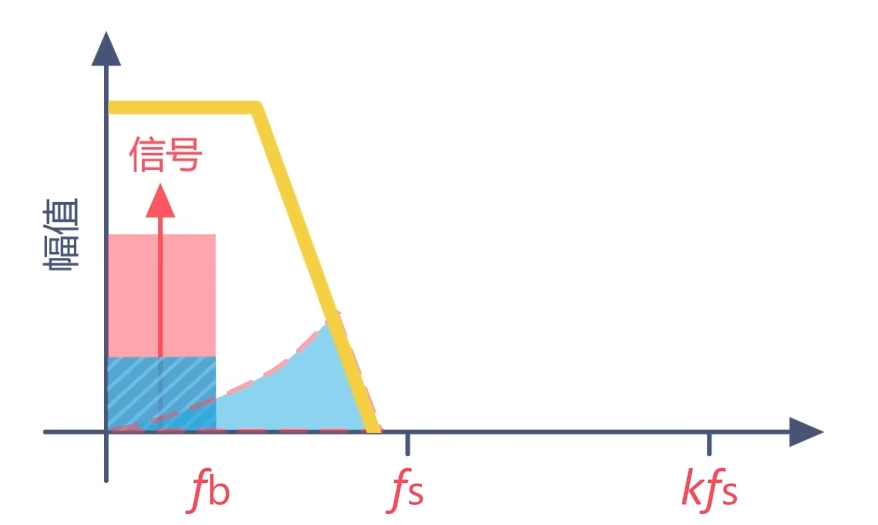
那么这两种技术又是如何实现的呢？我们假设，信号的带宽是Fb，采样频率为Fs。那么量化噪声会均匀分布在采样频率（Fs）上。图中的蓝色矩形表示量化噪声分布。
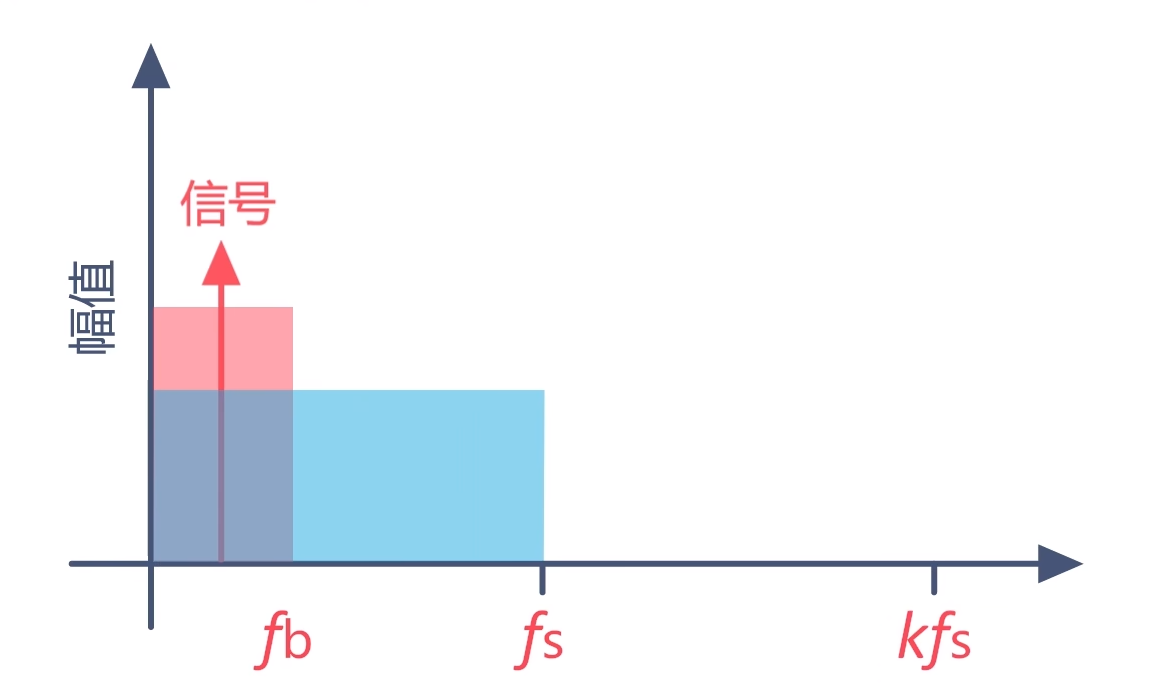
这时我们增大采样频率到K倍Fs，量化噪声依旧会均匀分布在采样频率（KFs）上。不过在信号带宽Fb内的量化噪声相对来说就减小了。
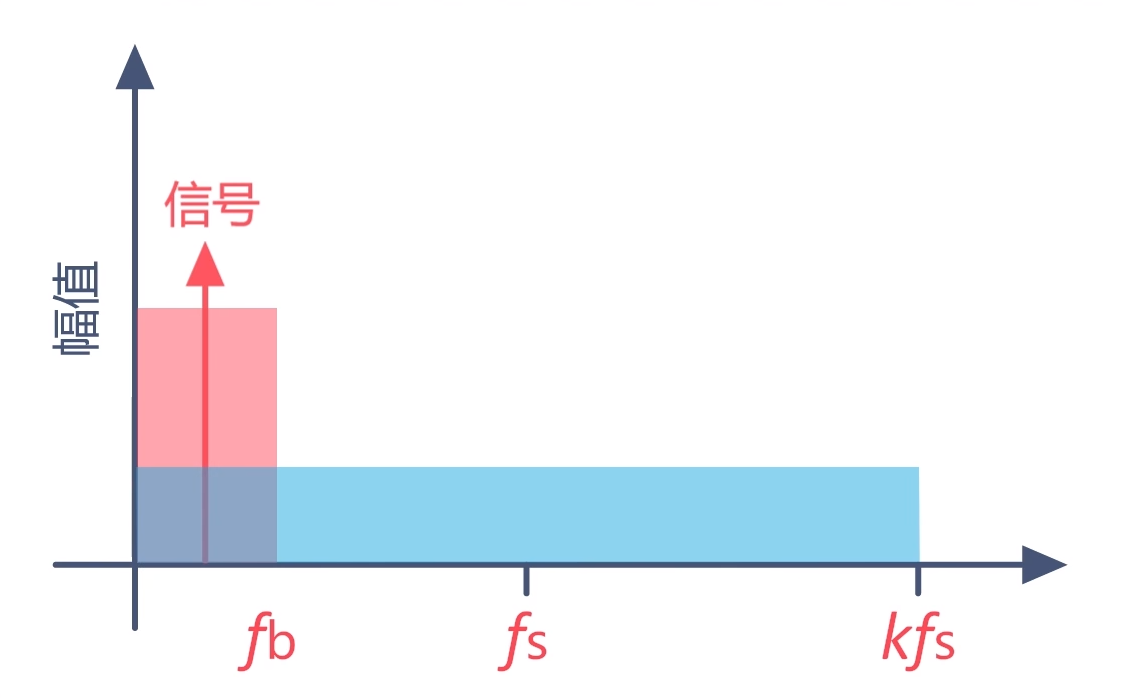
然后再让它通过一个低通滤波器，那么就可以把输出信号中大部分的量化噪声滤除。
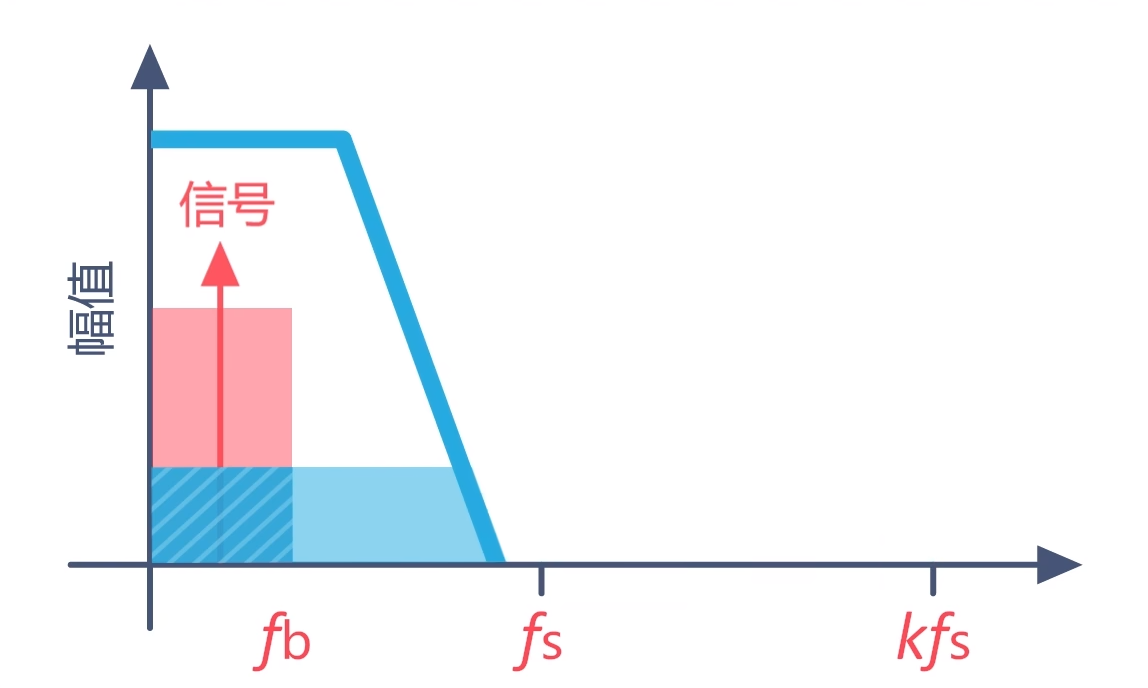
也就是通常所说的提高了信号的信噪比。信噪比是指系统输入的信号功率与系统引起的噪声功率之比，越大越好。这里要额外说明的是：过采样后通过低通滤波器是Σ-ΔADC中数字抽取滤波器部分的功能，调制器输出的仍是带有高频量化噪声的信号。
过采样技术的问题是采样频率越高，消耗的硬件资源就越多，所以其采样频率不可能无限拔高。如何使信号带宽内的量化噪声更少呢？工程师们又引入了噪声整形技术。其基本想法是将低频段的量化噪声尽量搬移到高频段。相当于将过采样后的信号通过一个高通滤波器，将平均分布在采样频率上的噪声，整形成低频段功率小，高频段功率大的形状。
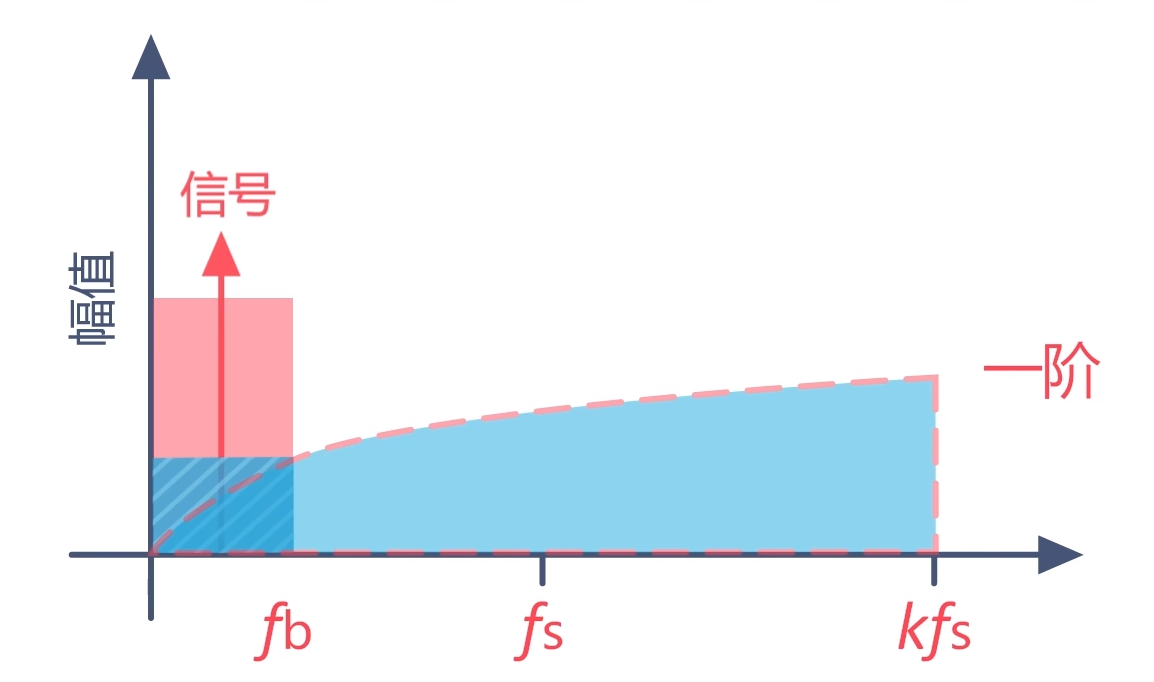
当然如果我们选择更多阶的调制，噪声整形的效果会更加明显，分辨率相应的也会更高。
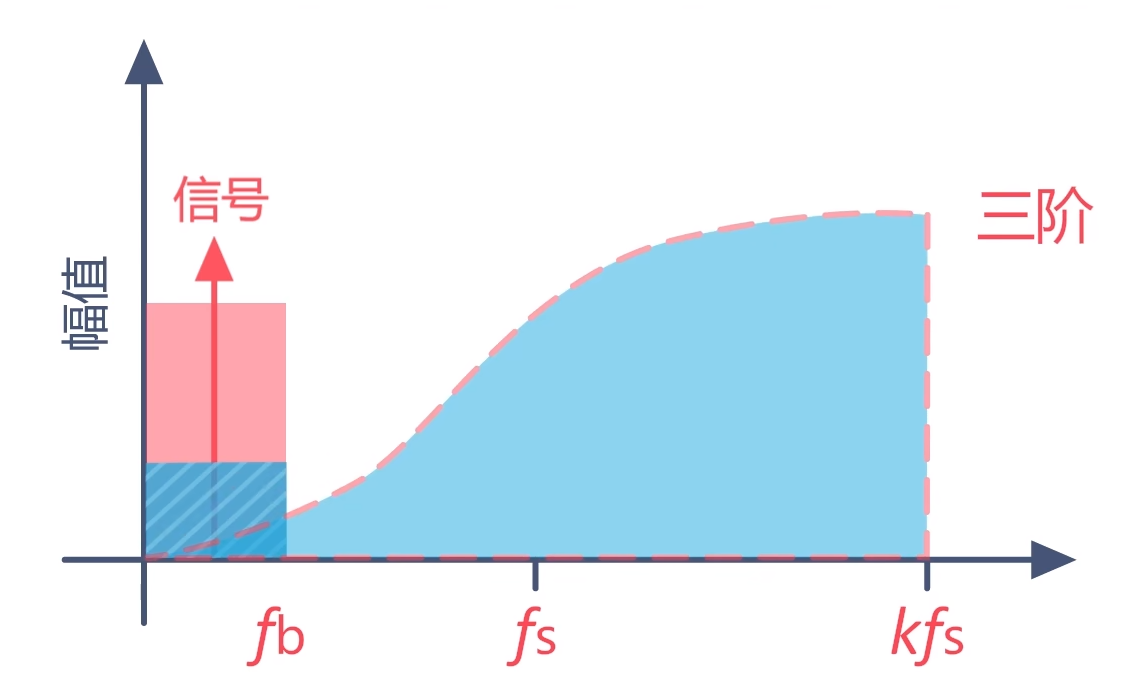
最终Σ-Δ调制器输出的是这样一个信号：信号带宽内的噪声很小，量化噪声大部分被搬移到了高频部分。这里给出的是调制器输出信号的频域谱图，实际输出信号应该是时域范畴的，波形如图所示：
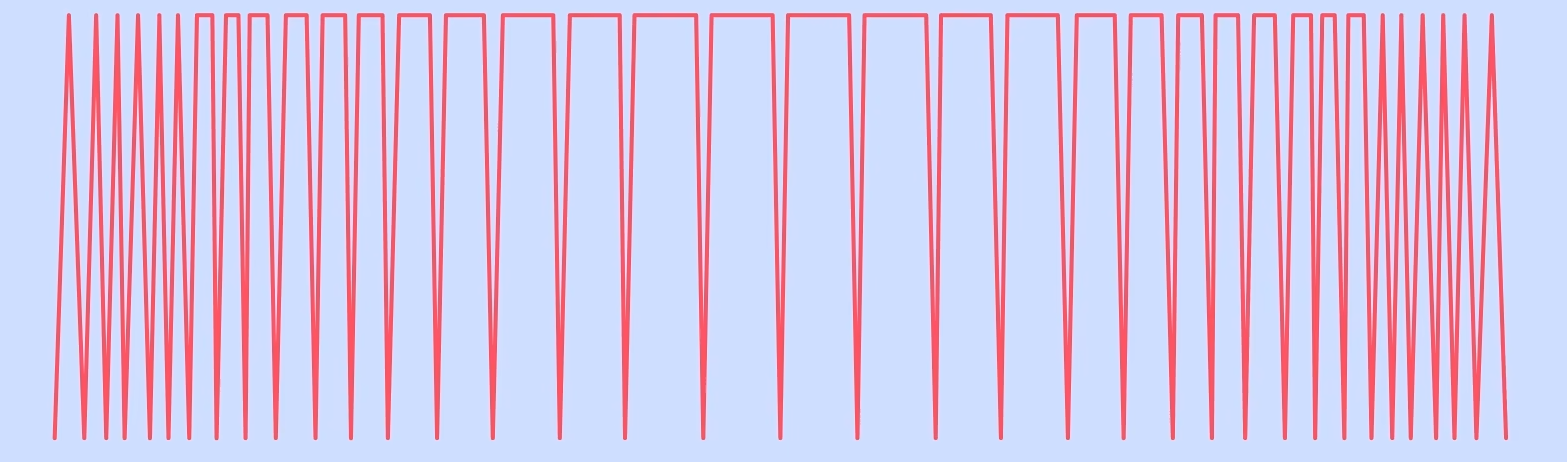
这个信号带有高频噪声，同时速率很高，会对之后的信号处理造成不小的压力。所以，我们要把它输入到数字抽取滤波器中，过滤掉高频的量化噪声。
然后再通过降采样的方式，降低信号的速率，以方便信号处理。这样就完成了最终的信号输出。
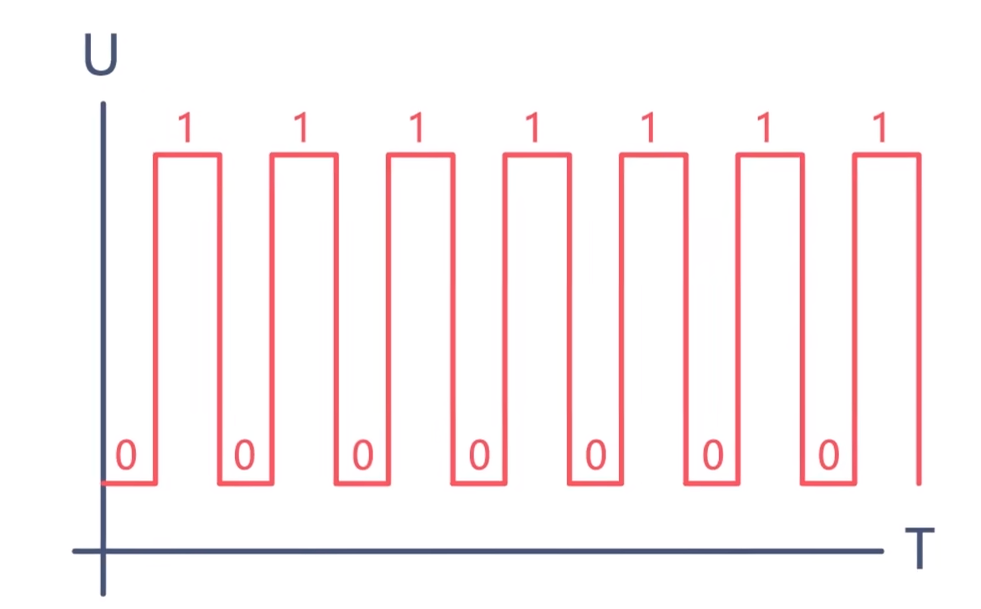
Σ-Δ ADC的优点是易于集成，而且分辨率高达24bit，甚至更高，但它的缺点是响应时间较长，功耗也会高一点。在音频分析、测量等方面应用广泛。
视频中介绍了三种常见的ADC。就采样速度来讲，Piepline ADC是最快的，SAR ADC中等，Σ-Δ ADC稍差。但从精度方面看，Σ-Δ ADC的精度普遍更高，SAR ADC中等，Piepline ADC就低一些。
以上就是Smacq对模数转换器（ADC）的相关介绍。如果对于文章内容有任何问题，都欢迎您在评论区留言或搜索我们的微信公众号“Smacq思迈科华”直接联系我们。文章的视频版内容可以点击如下链接跳转：ADC——模数转换器的基础知识和几个常见类型。
感谢您的阅读，希望您点赞、评论、转发。我们下期再见。
审核编辑 黄宇
